Влияние вязкого трения

Общее решение. Основное уравнение вынужденных колебаний с учётом вязкого трения принимает вид

                                         (106)

где

Оно отличается от соответствующего уравнения при свободных колебаниях наличием правой части, а от уравнения вынужденных колебаний системы без трения - наличием второго слагаемого в левой части. Для получения общего решения воспользуемся способом, который применялся выше при решении подобной задачи для n =  0.

Пусть к системе с одной степенью свободы в момент времени

 прикладывается мгновенный импульс; последующий колебательный процесс можно описать уравнением

                                    (107)

Определим постоянные А и

 из условий начала движения: при  должно быть Х=0,  Первое условие даёт

Из второго условия найдём

где 

.

Таким образом, свободные колебания, вызванные импульсом S, описываются законом

и носят затухающий характер.

Как и выше, будем рассматривать возмущающую силу

 в виде последовательности бесконечно малых импульсов . Тогда общее решение задачи о действии силы F(t) принимает вид

,                            (108)

причём закон изменения силы F(t) может быть любым.

Гармоническая возмущающая сила.  В практически важном случае действия гармонической силы

 решение  (108) даёт

                                         (109)

где

                                       (110)

                                           (111)

Введём, как и выше, динамический коэффициент

                                (112)

Динамический коэффициент

 не обращается в бесконечность ни при каких значениях частоты возмущения p; этим найденный результат существенно отличается от решения, полученного выше без учёта неупругого сопротивления. Зависимость  от отношения частот  при различных значениях отношения  приведена на рис. 45,a. Максимум динамического коэффициента несколько смещён в сторону от абсциссы  Однако это смещение мало, и можно приближённо определять  подставляя в (112)  т.е. .

Отсюда видно, что максимум динамического коэффициента обратно пропорционален коэффициенту затухания n.
Из графиков (рис.45,a) следует, что силы вязкого сопротивления оказывают заметное влияние только в околорезонансной области. Это позволяет в удалении от резонанса принимать для

 кривую, построенную без учёта вязкого сопротивления (рис. 41,a), а во всей околорезонансной области принимать .



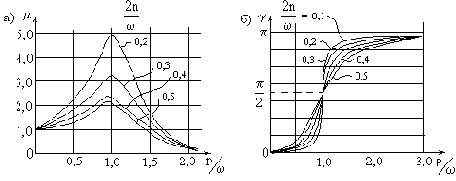
Рис. 45

Рассмотрим вопрос о "запаздывании" колебаний. Фазовый угол  определяется (111) и зависит от отношения частот   (рис. 45,б).

Как видно, при малых частотах p угол  невелик. При резонансе  фазовый угол равен ,  т.е. в те мгновения, когда сила максимальна, перемещение равно нулю. При высоких частотах фазовый угол близок к , т.е. максимуму силы соответствует максимум перемещения.

Действие периодических импульсов. В качестве исходного выражения примем вместо (104) закон свободных затухающих колебаний

.                (113)

Дифференцируя, получим выражение скорости

.

Начало отсчёта совместим с временем  (рис.44,б). Для мгновения  можно записать

;

.

В мгновение   перемещение и скорость вновь равны   и

              (114)

где S- величина импульса.

Из (114) находим

                         (115)

Вычислив  и ,  можно по  (113) найти решение х.

Особый интерес представляют резонансные режимы, при которых период импульсов T в целое число раз больше собственного периода колебаний . Обозначим это число через .

 .

Тогда

      ,

и по (115) находим

; .

При малых значениях  можно считать

 т.е. ,

и решение имеет вид

.

Наибольшее значение (резонансная амплитуда) приблизительно составляет

,

т.е. оказывается обратно пропорциональным коэффициенту вязкого сопротивления (как и в случае гармонического возмущения). Коэффициент повторности при резонансе получим, разделив  на амплитуду колебаний, вызванных однократным ударом :

,

т.е. с увеличением r (уменьшением частоты импульсов) резонансные амплитуды убывают.


Содержание раздела

---

---