Вязкое трение

В этом случае возникает сопротивление движению, которое пропорционально его скорости. При этом сила сопротивления описывается выражением

, (14)

где k- коэффициент пропорциональности.

Примером системы, работающей в условиях вязкого трения, может служить гидравлический амортизатор (рис.15), который создаёт сопротивление движению поршня, зависящее не от перемещения (как это свойственно упругим связям), а от скорости и пропорционально её первой степени (14). Подобные устройства применяются, например, в конструкциях автомобильной подвески. Гидравлический амортизатор состоит из одного или нескольких цилиндров с поршнями или из камеры, в которой может вращаться крыльчатка. Цилиндры и камера наполнены амортизационной жидкостью. При движении поршней или крыльчатки эта жидкость продавливается через калиброванные отверстия; этим создаётся сопротивление, по характеру близкое к вязкому. В формуле (14) R- это сила, действующая на амортизатор, а вязкая реакция амортизатора на колеблющееся тело имеет противоположное направление.

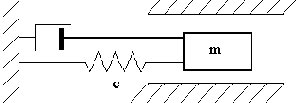
Рис. 15

Дифференциальное уравнение движения в рассматриваемом случае таково:

, (15)

или

, (16)

где

;

Для рассматриваемого линейного дифференциального уравнения с постоянными коэффициентами характеристическое уравнение имеет вид

Обозначим

Тогда решение уравнения (16) определяется формулой

(17)

или

, (18)

где

;

Следовательно, при наличии вязкого трения движение груза описывается непериодическим законом (рис. 16).

Тем не менее часто это движение называют периодическими затухающими колебаниями, несмотря на очевидную невозможность совмещения понятий "периодические" и "затухающие".

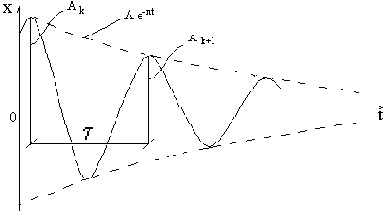
Рис. 16

Под периодом

этих колебаний понимают время между двумя максимальными смещениями:

. (19)

Величину

называют угловой частотой затухающих колебаний.

Отношение двух последовательных максимальных отклонений от положения равновесия

. (20)

Значит, последовательные максимальные отклонения системы от равновесного положения (амплитуды колебаний) представляют собой члены геометрической прогрессии со знаменателем, равным

. Чаще рассматривают не отношение двух последовательных амплитуд, а логарифм этого отношения, который называют логарифмическим декрементом колебаний:

. (21)

В металлических конструкциях без специально введенных элементов трения логарифмический декремент составляет обычно от нескольких сотых до десятых долей единицы.

Если колебания затухают медленно и отношение двух последовательных амплитуд

близко к единице, то

,

где

;

.

Таким образом, при малом затухании логарифмический декремент примерно равен отношению изменения амплитуды колебаний за период

к амплитуде

А.

Так как логарифмический декремент колебаний

,

то

.

Подставляя значение n2 в формулу для

, установим связь между величинами

. (22)

Из (22) следует, что даже при значительном затухании частота

затухающих колебаний мало отличается от частоты

собственных колебаний соответствующей системы без трения. Например, при сравнительно большом затухании, когда каждый следующий размах вдвое меньше предыдущего (

), частота

лишь на 0,6 % меньше, чем

. Таким образом, можно считать, что трение практически не влияет на частоту колебаний и

.

Определим постоянные интегрирования в решении уравнения затухающих колебаний (17). Обозначим смещение и скорость в начальный момент времени t0=0 через x0 и

соответственно. После подстановки в (17) получим

x0=C1;

,

тогда

C1=x0;

,

и решение уравнения (16) , удовлетворяющее начальным условиям, имеет вид

(23)

Пример 5. Амплитуда собственных колебаний за один период уменьшилась в два раза.Определить логарифмический декремент колебаний и изменение собственной частоты вследствие затухания.

Решение.

Логарифмический декремент колебаний:

;

,

откуда

.

Собственная частота колебаний:

,

т. е. изменение собственной частоты вследствие затухания составляет 0,6 %.

Содержание раздела