Свободные колебания стержневых систем

С изгибными свободными колебаниями многомассовых стержневых систем часто приходится сталкиваться в строительных конструкциях, а также в турбинах, где применяют валы с прямолинейной осью, несущие ряд дисков.

В качестве примера такой системы рассмотрим шарнирную балку с тремя сосредоточенными массами

(рис. 25,а).

Для таких систем при составлении уравнений движения удобнее использовать обратный способ, основанный, как уже говорилось, на введении сил инерции, приложенных к безмассовому упругому "скелету" системы. При этом удобно использовать понятие единичного перемещения

как перемещения в направлении i, вызванного безразмерной единичной силой, действующей в направлении k (рис. 25,б).

Если на систему по k-му направлению действует сила

и требуется определить вызванное ею полное перемещение в i-м направлении, то вследствие пропорциональности между силой и перемещением (справедлив закон Гука) можно записать, что

. При одновременном действии сил

полное перемещение по i-му направлению определяется суммированием

а б

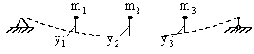
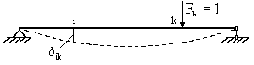
Рис. 25

Итак, рассмотрим свободные колебания балки, несущей сосредоточенные массы

(рис. 25,а). Развиваемые ими силы инерции

являются единственной нагрузкой на упругий "скелет" системы в процессе колебаний. Можно составить следующие выражения для перемещений точек приложения сосредоточенных масс под действием этих сил инерции:

(60)

Перемещения

вычисляются, как обычно, методами О. Мора или А.Н. Верещагина от единичных сил, приложенных в местах действия сил инерции, т.е. в сечениях, где находятся сосредоточенные массы.

Система дифференциальных уравнений (60) имеет частное решение в виде

(61)

Вторые производные этих перемещений по времени, т.е. ускорения, выражаются так:

(62)

Подставляя (61) и (62) в систему уравнений (60) и сокращая на

, после простейших преобразований получим

(63)

Отбрасывая тривиальное решение этой системы уравнений

как не отвечающее физическому смыслу рассматриваемой задачи, будем искать ненулевое решение исходя из условия равенства нулю определителя системы (63):

. (64)

Частотное уравнение, получаемое при раскрытии определителя (64) при числе степеней свободы системы

, может быть решено строго непосредственно. При

получение решения может оказаться затруднительным или даже невозможным.

Если направления перемещений

выбраны так, что побочные перемещения

обращаются в нуль, то система дифференциальных уравнений (60) и соответствующее ей уравнение частот распадаются на отдельные уравнения, содержащие только главные перемещения

. В этом случае перемещения

называются главными координатами, а соответствующие формы колебаний - главными формами колебаний.

Главные формы колебаний обособлены друг от друга и каждая из них происходит со своей определённой частотой, которая выражается формулой, аналогичной формуле для вычисления собственной частоты системы с одной степенью свободы

.

Выбор главных координат для систем с числом степеней свободы, большим двух, в общем случае весьма затруднителен. При

это возможно всегда.

Для симметричных систем с симметрично расположенными массами возможны прямо симметричные и обратно симметричные формы колебаний, при которых силы инерции будут соответственно прямо симметричны и обратно симметричны. В этом случае перемещения вычисляются как групповые от парных прямо симметричных или обратно симметричных единичных сил. Побочные перемещения, связывающие прямо симметричные и обратно симметричные силы инерции, обращаются в нуль. Это также приводит к распаду частотного уравнения на два независимых уравнения, из которых одно позволяет найти частоты прямо симметричных колебаний, а другое - обратно симметричных. Так как групповые перемещения определяются от парных единичных сил, то соответствующая масса должна входить в частотные уравнения с коэффициентом 0,5.

Содержание раздела