Свободные колебания систем с конечным числом степеней свободы (общий случай)

Как уже говорилось (см. подразд. 1.4), дифференциальные уравнения движения таких систем можно получить тремя основными способами: 1) в форме уравнений Лагранжа; 2) прямым способом;  3) обратным способом.

Наиболее общий вид дифференциальных уравнений движения может быть получен в форме уравнений Лагранжа

,                                        (29)

где K и П - кинетическая и потенциальная энергии соответственно;

 и - обобщённые ко­ординаты и обобщённые скорости; число степеней свободы системы.

Известно, что при малых колебаниях около положения равновесия кинетическая и потенци­альная энергии выражаются через обобщённые координаты и обобщённые скорости следующим образом:

                  

; ,                            (30)            

где

инерционные коэффициенты; квазиупругие коэффициенты, называемые также обобщёнными коэффициентами жёсткости.

Подставляя (30) в (29), получим систему однородных линейных дифференциальных уравне­ний с постоянными коэффициентами:

,        (31)

Однако составление уравнений движения по схеме Лагранжа не является обязательным, потому что во многих случаях прямой или обратный способы оказываются более удобными.

Рассмотрим особенности названных способов на примере системы с двумя степенями сво­боды, состоящей из тел с массами

и ,соединённых пружинами с жесткостями и (рис. 22,а).

За обобщённые координаты примем горизонтальные перемещения

игрузов, отсчиты­ваемые от положения равновесия, в которых отсутствуют деформации пружин. Удлинения пружин в процессе движения: ; .

Основной способ (уравнения Лагранжа)

Кинетическая энергия рассматриваемой системы:

.

Потенциальная энергия деформации пружин:

.

Вычислим производные, необходимые для подстановки в уравнения Лагранжа:

; ;

; ;

; .

Подставляя вычисленные значения в (29), получим дифференциальные уравнения движения рассматриваемой системы

             

                                            (32)  

Прямой способ

 Выделяем массы

и и рассматриваем их как свободные тела под дейст­вием сил упругости, определяемых удлинениями и обеих пружин (рис. 22,б):

 

Дифференциальные уравнения движения грузов имеют вид



Подставляя значения и , получим



т.е. эти уравнения совпали с уравнениями (32).

а                                                                         б

      

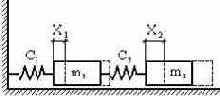
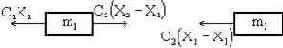
в



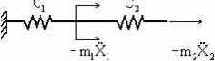
Рис. 22




Содержание раздела

---

---

---

Главная сайта

---