Свободные колебания автомобиля
Рассмотрим автомобиль как систему упругосвязанных между собой жестких тел (рис. 32,а). Здесь тело 1 схематически представляет собой кузов автомобиля, тела 2-5 - колеса, массы которых будем считать сосредоточенными.
Движение такой системы в процессе колебаний характеризуется семью координатами:




Распределение масс автомобиля и жестокостей упругих связей почти симметрично относительно средней продольной плоскости, поэтому в расчетах колебаний некоторой малой асимметрией можно пренебречь. При этом общий процесс колебаний можно рассматривать состоящим из двух взаимно не связанных процессов (рис. 32,б,в): продольных колебаний, характеризуемых вертикальным перемещением кузова







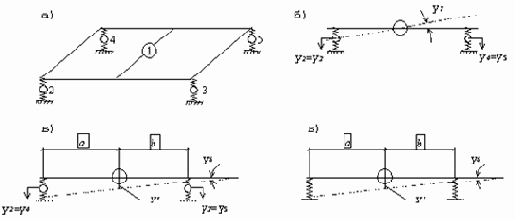
Рис. 32
В соответствии с этим продольные колебания описываются четырьмя, а поперечные колебания - тремя дифференциальными уравнениями.
Рассмотрим продольные колебания, которые имеют основное значение.
Обозначим жесткости шин через С; жесткости передних и задних рессор через СП и СЗ соответственно; массы кузова и колеса - через m и mК. Радиус инерции кузова относительно поперечной оси, проходящей через его центр тяжести, обозначим через

Тогда деформации рессор составляют


Уравнения движения составим на основе уравнений Лагранжа.
Кинетическая энергия системы складывается из следующих частей:
кинетической энергии кузова

кинетической энергии передних колес

кинетической энергии задних колес

Суммарная кинетическая энергия:

Потенциальная энергия деформации рессор:

Потенциальная энергия сжатия шин:

Суммарная потенциальная энергия:

Вычисляя соответствующие производные и подставляя в уравнения Лагранжа (29), получим

Частное решение системы (73) имеет вид

Подстановка частного решения в уравнение (73) приведет, как в рассмотренных ранее системах, к однородным относительно амплитуд

С практической точки зрения удовлетворительный результат дает рассмотрение упрощенной схемы продольных колебаний (рис. 32,г).
Будем считать шины недеформируемыми, тогда рассматриваемая система обладает двумя степенями свободы, соответствующими координатам



Уравнения Лагранжа:

Частное решение

После его подстановки получим

или

Как обычно, для получения нетривиального решения приравниваем нулю определитель системы:

Раскрывая определитель, получим частотное уравнение в виде

Определив из уравнения (75) собственные частоты, можно найти соответствующие им собственные формы колебаний. Для этого из какого-либо (например, из первого) уравнения системы (74) нужно образовать отношение амплитуд

и подставить в него поочередно оба корня частотного уравнения.
Рассмотрим подробно частный случай такого распределения масс, при котором


Для определения собственных форм колебаний подставим эти корни поочередно в соотношение (76). Тогда для первой собственной формы получим

а для второй собственной формы -

Эти формы колебаний представлены на рис. 33,а,б. Их особенностью является неподвижность одной оси автомобиля при колебаниях другой. Формулы (77) показывают, что в этом частном случае частоты можно вычислять, используя схему, показанную на рис.33,в, т.е.
распределяя общую массу по закону рычага.
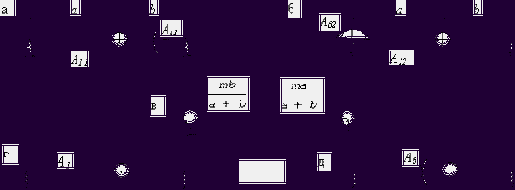
Рис. 33
В другом частном случае, когда Спа = СЗb, уравнения (74) становятся независимыми

что означает возможность чисто вертикальных колебаний при отсутствии поворотов - «подпрыгивание» (рис. 33,г), а также чисто угловых колебаний при неподвижности центра тяжести - «галопирование» (рис. 33,д). Действительно, система (78) удовлетворяется решением



и решением


Из (79) находим первую собственную частоту:

а из (80) - вторую собственную частоту:

Пример 11. Определить собственные частоты и собственные формы колебаний автомобиля, для которого известно:

