Стержневые системы с конечным числом степеней свободы при гармоническом нагружении

При действии на упругую систему (балку или раму) с конечным числом степеней свободы вибрационной гармонической нагрузки изгибающие моменты, поперечные и продольные силы также будут изменяться во времени, а их наибольшие значения (амплитуды) будут зависеть от частот возмущающих сил. Если все возмущающие нагрузки, действующие на систему, имеют одну и ту же частоту р и изменяются в одной фазе, то силы инерции, а следовательно, и изгибающие моменты, поперечные и продольные силы достигают наибольших значений в одно и то же время.

Для решения задачи о вынужденных колебаниях стержневой системы можно использовать как метод сил, так и метод перемещений, причём наибольшее применение в расчётной практике находит первый из указанных методов.

 Метод сил. Рассмотрим упругую систему (рис.50) с конечным числом сосредоточенных масс, на которую действуют вибрационные силы

.

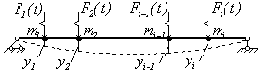
Рис. 50

Перемещение любой массы

 в произвольный момент времени выражается в виде

,                      (135)

где

силы инерции соответствующих масс;     перемещения по направлению силы инерции , вызванные единичными  силами , приложенными в точках нахождения соответствующих  масс; перемещение точки расположения массы  от действия амплитудных значений всех  приложенных вибрационных нагрузок.

Перечисленные перемещения вычисляются путём перемножения соответствующих эпюр методом Мора-Верещагина.

С другой стороны, при гармонических вынужденных колебаниях с

частотой р перемещение массы

 и её ускорение можно записать в виде

Сила инерции массы

:

  

,

отсюда

                                             (136)

Подставляя (136) в (135), после простейших преобразований получим

,

где

.

Записывая аналогичные уравнения для каждой из сосредоточенных масс, получим систему уравнений, которая называется системой канонических уравнений динамического варианта метода сил:

                     (137)

где

число степеней свободы системы.

Уравнения (137) позволяют определить наибольшие (амплитудные) значения сил инерции.

Сама система уравнений (137) по форме аналогична системе канонических уравнений метода сил, используемого при расчёте статически неопределимых систем, но неизвестными в ней являются не реакции отброшенных связей в статически неопределимой системе, а амплитуды сил инерции масс, которые могут возникать как в статически определимой, так и в статически неопределимой системах.

После вычисления максимальных значений сил инерции  эпюра динамических изгибающих моментов строится путём сложения единичных эпюр, предварительно умноженных на найденные значения соответствующих инерционных сил, с эпюрой , т.е. в соответствии с выражением

.

Использование симметрии системы при её расчёте на вынужденные колебания оказывается возможным только при симметричном расположении масс.



Рис. 51

При несимметричной вибрационной нагрузке разложение сил инерции на симметричные и обратно симметричные группы (рис.51) приводит к распаду системы канонических уравнений на две независимые системы.

В этом случае вычисление главных перемещений по направлению парных неизвестных нужно вести по формуле

.

При симметричной вибрационной нагрузке все обратно симметричные силы инерции равны нулю, а при обратно симметричной вибрационной нагрузке симметричные силы инерции равны нулю. Симметричная нагрузка может привести к резонансу только при совпадении её частоты с собственными частотами симметричных колебаний системы и, наоборот, обратно симметричная нагрузка может дать резонанс только с частотами обратно симметричных свободных колебаний.

Метод перемещений. Этому методу отдают предпочтение при расчёте рам на вынужденные колебания. Рассмотрим систему (рис.52,а), для которой основная система получается путём введения связей по направлению неизвестных перемещений  соответствующих масс  (рис.52,б).

а                                                                б

           

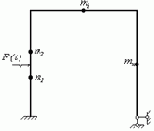
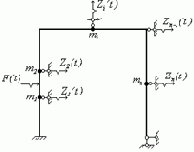
Рис. 52

Уравнение, выражающее равенство нулю динамической реакции введённой связи по направлению любого перемещения  с учётом силы инерции , выражается в виде



.

Учитывая, что при гармонических колебаниях , получим систему уравнений

                               (138)

где

.

Строго говоря, неизвестные  и свободные члены   являются величинами переменными, изменяющимися одновременно и по одному и тому же закону, характеризуемому множителем , к их амплитудным значениям. Так как этот множитель присутствует во всех членах системы (138), то на него может быть произведено сокращение. Тогда неизвестные и свободные члены уравнений (138) должны рассматриваться в качестве соответствующих амплитудных значений.

 Реакции  определяются от единичных перемещений основной системы, приложенных в тех сечениях, где находятся точечные массы, т.е. так же, как и при определении частот свободных колебаний.

 Реакции от амплитудных значений вибрационных нагрузок  определяются в основной системе.

 После вычисления неизвестных амплитуд перемещений  эпюра динамических изгибающих моментов строится в соответствии с выражением

 ,

где  эпюры изгибающих моментов в основной системе от соответствующих единичных перемещений; эпюра моментов в основной системе от амплитудных значений вибрационных нагрузок.

Система уравнений (138) по своей структуре аналогична системе канонических уравнений метода перемещений, применяемого для расчёта статически неопределимых систем, но здесь неизвестные  являются не искомыми перемещениями узлов рамы, а амплитудами перемещений сосредоточенных масс.

Так же как и метод сил, метод перемещений может быть использован не только для систем, совершающих изгибные вынужденные колебания, но и для систем, испытывающих продольные вынужденные колебания.


Содержание раздела

---

---