Продольные колебания стержней

При анализе продольных колебаний прямолинейного стержня (рис.67,а) будем считать, что поперечные сечения остаются плоскими и что частицы стержня не совершают поперечных движений, а перемещаются только в продольном направлении.

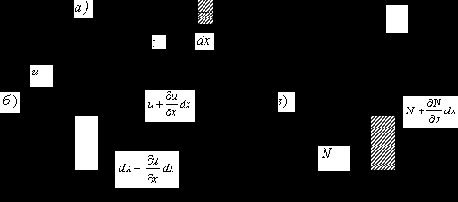
Рис. 67

Пусть u - продольное перемещение текущего сечения стержня при колебаниях; это перемещение зависит от расположения сечения (координаты x) и от времени t. Таким образом,

есть функция двух переменных; её определение и представляет основную задачу. Перемещение бесконечно близкого сечения равно

, следовательно, абсолютное удлинение бесконечно малого элемента

равно

(рис.67,б), а относительное его удлинение

Соответственно продольная сила в сечении с координатой х может быть записана в виде

, (173)

где

жёсткость стержня при растяжении (сжатии). Сила N также является функцией двух аргументов – координаты х и времени t.

Рассмотрим элемент стержня, расположенный между двумя бесконечно близкими сечениями (рис.67,в). К левой грани элемента приложена сила N, а к правой – сила

. Если обозначить через

плотность материала стержня, то масса рассматриваемого элемента составляет

. Поэтому уравнение движения в проекции на ось х

или

. (174)

Учитывая (173) и принимая A = const , получим

, (175)

где

. (176)

Следуя методу Фурье, ищем частное решение дифференциального уравнения (175) в виде

, (177)

т.е. предположим, что перемещение u можно представить в виде произведения двух функций, одна из которых зависит только от аргумента х, а другая только от аргумента t. Тогда вместо определения функции двух переменных u (x, t) необходимо определять две функции X(x) и T(t), каждая из которых зависит только от одной переменной.

Подставив (177) в (174), получим

где штрихами обозначена операция дифференцирования по x, а точками – по t.
Перепишем это уравнение таким образом:

.

Здесь левая часть зависит только от x,а правая – только от t. Для тождественного выполнения этого равенства (при любых x и t) необходимо, чтобы каждая из его частей была равна постоянной, которую обозначим через

;

. (178)

Отсюда следуют два уравнения:

;

. (179)

Первое уравнение имеет решение:

, (180)

указывающее на колебательный характер, причём из (180) видно, что неизвестная величина

имеет смысл частоты свободных колебаний.

Второе из уравнений (179) имеет решение:

, (181)

определяющее форму колебаний.

Частотное уравнение, определяющее величину

, составляется путём использования граничных условий. Это уравнение всегда трансцендентное и имеет бесконечное число корней. Таким образом, число собственных частот бесконечно, причём каждому значению частоты

соответствует своя функция Tn(t), определяемая зависимостью (180), и своя функция Xn(x), определяемая зависимостью (181). Решение (177) является лишь частным и не даёт полного описания движения. Полное решение получается путём наложения всех частных решений:

.

Функции Xn(x) называются собственными функциями задачи и описывают собственные формы колебаний. Они не зависят от начальных условий и удовлетворяют условию ортогональности, которое при А=const имеет вид

, если

.

Рассмотрим некоторые варианты граничных условий.

Закреплённый конец стержня (рис.68,а). В концевом сечении перемещение u должно быть равно нулю; отсюда следует, что в этом сечении

X=0 (182)

Свободный конец стержня (рис.68,б). В концевом сечении продольная сила

(183)

должна тождественно равняться нулю, что возможно, если в концевом сечении X'=0.

Упругозакреплённый конец стержня (рис.68,в).

При перемещении u концевого стержня возникает упругая реакция опоры

, где Со - жёсткость опоры.

Учитывая (183) для продольной силы, получим граничное условие

,

если опора расположена на левом конце стержня (рис.68,в), и

,

если опора расположена на правом конце стержня (рис.68,г).

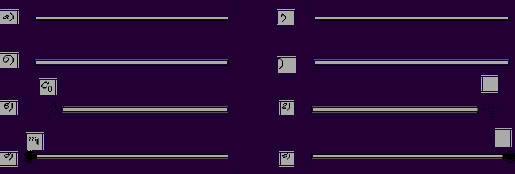
Рис. 68

Сосредоточенная масса

на конце стержня.

Развиваемая массой сила инерции:

.

Так как, согласно первому из уравнений (179),

, то сила инерции может быть записана в виде

. Получаем граничное условие

,

если масса находится на левом конце (рис.68,д), и

, (184)

если масса связана с правым концом (рис.68,е).

Определим собственные частоты консольного стержня (рис.68,a').

Согласно (182) и (183), граничные условия

X=0 при х=0;

X'=0 при х=

.

Подставляя поочерёдно эти условия в решение (181), получим

D=0;

.

Условие С

0 приводит к частотному уравнению:

.

Корни этого уравнения

(n=1,2,…)

определяют собственные частоты:

(n=1,2,…). (185)

Первая (низшая) частота при n=1:

.

Вторая частота (при n=2):

и т. д.

Определим собственные частоты стержня с массой

на конце (рис.68,е).

Согласно (182) и (184), имеем

X=0 при х=0;

при х=

.

Подставляя эти условия в решение (181), получим:

D=0;

.

Следовательно, частотное уравнение при учёте (176) имеет вид

.

Здесь правая часть представляет собой отношение массы стержня к массе концевого груза.

Для решения полученного трансцендентного уравнения необходимо воспользоваться каким-либо приближённым способом.

При

значения наиболее важного низшего корня

будут соответственно 0.32 и 0.65 .

При малом отношении

решающее влияние оказывает груз и хорошие результаты даёт приближённое решение

.

Для стержней переменного сечения, т.е. при А

const, из (173) и (174) получается уравнение движения в виде

.

Это дифференциальное уравнение не поддаётся решению в замкнутом виде. Поэтому в подобных случаях приходится прибегать к приближённым методам определения собственных частот.

Содержание раздела