К цилиндрической пружине подвешен груз

Пример 1. К цилиндрической пружине подвешен груз массой
m = 2 кг = 2

. Груз может перемещаться только в вертикальном направлении. Определить частоту собственных колебаний груза без учёта и с учётом массы пружины. Средний диаметр пружины D = 6 см; диаметр проволоки пружины d = 0,6 см; число витков n = 15; плотность материала

; модуль сдвига G =

.
Решение.
Жесткость пружины:

.
Частота собственных колебаний без учёта массы пружины :

.
Приведенная масса пружины:

Частота собственных колебаний с учётом массы пружины:

.
Пример 2. Определить круговую и техническую частоту, а также период собственных колебаний сосредоточенного груза Р = 12 кН, приложенного на свободном конце балки, жестко заделанной другим концом. Балка представляет собой двутавр № 20 (Jx = 1840 см4) длиной

= 1 м. Собственным весом балки пренебречь.
Решение.
Статический прогиб балки от веса сосредоточенного груза:

.
Частота собственных колебаний:

.
Период колебаний:

.
Техническая частота:

.
Пример 3. К стальному стержню подвешен груз массой m = 50 кг, совершающий вертикальные продольные колебания. Длина стержня

= 1 м, диаметр d = 2 см. Определить частоту и период собственных вертикальных колебаний системы без учёта и с учётом массы стержня.
Решение.
Жесткость стержня:

.
Частота собственных колебаний без учёта массы стержня:

.
Соответствующий период колебаний:

.
Приведенная масса стержня:

.
Собственная частота колебаний с учётом массы стержня:

.
Соответствующий период колебаний:

.
Пример 4.
Определить собственную частоту крутильных колебаний двухмассовой системы (рис. 14,а) при следующих данных: диаметры дисков d1 =0,30 м; d2 = 0,20 м; толщины дисков b1 = 0,02 м; b2 = 0,015 м; диаметр вала d0 = 0,01 м; длина вала

= 0,8 м.

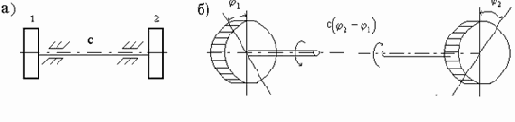
Рис. 14
Решение.
Дифференциальное уравнение свободных колебаний такой системы имеет вид

,
где

- взаимный угол поворота дисков,

- собственная частота колебаний.
Моменты инерции масс дисков:

;

.
Полярный момент инерции поперечного сечения вала:

.
Коэффициент жесткости вала при кручении:

.
Собственная частота крутильных колебаний:

.

Пример 6. Пружина несёт две массы

каждая - одна на конце пружины, другая посередине (рис. 28,а). Средний диаметр пружины

; диаметр проволоки пружины

; число витков на каждой половине пружины

. Определить частоты собственных колебаний системы.
а б

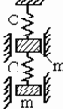
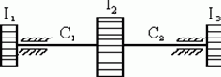
Рис. 28
Решение
Уравнения движения системы

где

- смещения верхней и нижней масс соответственно; С - жёсткость пружины.
Решение системы уравнений ищем в виде

После подстановки получим систему однородных алгебраических уравнений

Частотное уравнение

,
или

.
Корни частотного уравнения:

;

.
Жёсткость пружины:

.
Собственные частоты:

.
Пример 7. Определить частоты собственных колебаний невесомой консольной балки с двумя равными сосредоточенными массами (рис. 29,а). Построить собственные формы колебаний, проверить их ортогональность.

Пример №12. Ротор электродвигателя, установленного на консоли (рис.46,а), имеет частоту вращения n=900

Вследствие неуравновешенности ротора возникает вертикальная переменная сила

.Определить: 1) при каком значении

наступает резонанс; 2) на каком расстоянии

нужно установить двигатель, чтобы частота собственных колебаний балки была на 30 % больше частоты возмущающей силы. Для этого случая вычислить амплитуду вынужденных колебаний и максимальное нормальное напряжение. Массой балки пренебречь. Масса двигателя m=100 кг; амплитуда возмущающей силы

Содержание раздела