Позиционное трение

Так называется вид трения, при котором сила трения пропорциональна смещению. Рассмот­рим систему, состоящую из груза массой m, закреплённого на рессоре, листы которой собраны без предварительного натяга (рис. 20,а). Сила трения листов рессоры друг от друга пропорцио­нальна контактному давлению, которое, в свою очередь, пропорционально смещению

. Зави­симость между реакцией рессоры, действующей на груз, и смещением грузаF=¦для рассматриваемой системы представлена на рис. 20,б.

 Обозначим жёсткость системы при увеличении смещения

по модулю через С, а жёсткость при уменьшении абсолютного значения смещения - через С. Жёсткость упругого элемента системы при отсутствии трения

 С

.

а                                                          б             

             

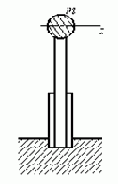
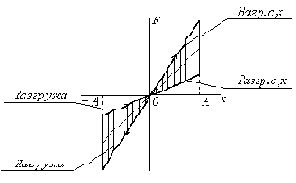
Рис. 20

На каждой четверти периода характеристика системы прямолинейна, поэтому движение массы m описывается синусоидой. При переходе через равновесное положение частота собст­венных колебаний меняется от

 до . Отклоним массу m в крайнее правое положение, при этом её скорость в этот момент . Если груз отпустить, то он начнёт дви­гаться влево под действием силы упругости, уменьшенной на величину сил трения. Частота собственных колебаний груза будет , а время движения до равновесного положения - . Скорость груза в равновесном положении станет равной . Дальнейшее движение (влево) определяется жёсткостью , а крайнего левого положения груз достигает че­рез время . Наибольшее смещение влево равно .

Максимальное отклонение вправо в конце полного периода движения вычисляется по формуле

=,

следовательно, логарифмический декремент колебаний:

=.

При малом затухании, когда разность жесткостей

существенно меньше средней жёст­кости , получим

.

Характер движения при позиционном трении показан на рис. 21. Из полученных формул сле­дует, что при силе трения, пропорциональной смещению, логарифмический декремент колебаний постоянен и, следовательно, точно так же, как и при вязком трении, последовательные ампли­туды составляют геометрическую прогрессию.

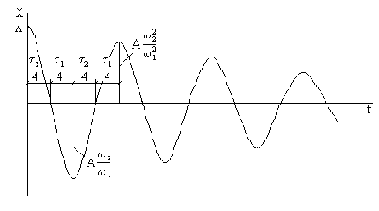
Рис. 21

Как видно из рис. 21, период рассматриваемых затухающих колебаний:

.

Соответствующая этому периоду угловая частота:

.

Частоты и  определяются выражениями

;

,

где - собственная частота соответствующей системы без трения.

Тогда

.

При небольших логарифмических декрементах колебаний  это выражение отличается от соб­ственной частоты колебаний соответствующей системы без трения на величину второго по­рядка малости. Поэтому подобно вязкому и сухому трению позиционное трение практически не влияет на собственную частоту колебаний.


Содержание раздела

---

---