Основное уравнение (уравнение Матье)
В ряде случаев параметры механической системы - ее жесткость или масса - не остаются неизменными, а являются некоторыми заданными функциями времени, чаще периодическими. Если нарушить состояние равновесия такой системы, то будут происходить своеобразные колебания: с одной стороны, их нельзя назвать свободными, так как система испытывает определенное внешнее воздействие в виде изменения жесткости, а с другой - они не являются вынужденными, так как внешнее воздействие не проявляется в виде заданной возмущающей силы. Эти колебания называются параметрическими и в зависимости от свойств системы и характера изменения ее параметров могут иметь ограниченные или возрастающие амплитуды, причем во втором случае возможно наступление параметрического резонанса.
Рассмотрим простейшую систему (рис.56). Сосредоточенная масса 1 закреплена на конце невесомого стержня 2. Свобода перемещений стержня дополнительно ограничена втулкой 3, удаленной от нижнего конца стержня на расстояние


Рис. 56
Составим уравнение свободных колебаний груза, считая, что они происходят в плоскости чертежа. Если в текущий момент времени t перемещение груза составляет x, то восстанавливающая сила упругости стержня равна -cx, а уравнение движения груза имеет вид

где c - коэффициент жесткости системы.
Втулка 3 при ее достаточной длине обеспечивает практически полное защемление нижней части стержня, и тогда



Если расстояние



Теперь предположим, что втулка 3 скользит вдоль стержня 2 по заданному закону

т.е. совершает около среднего положения



и дифференциальное уравнение (148) становится уравнением с переменными
коэффициентами:

что характерно для системы с параметрическим возбуждением колебаний.
Существует много других механических систем, подверженных параметрическому возбуждению. Ряд примеров убеждает, что в большинстве практически важных случаев дифференциальное уравнение параметрических колебаний можно привести к стандартной форме:

где a и q - некоторые постоянные.
Возвращаясь к механической системе, показанной на рис.56, положим, что амплитуда колебаний втулки A весьма мала по сравнению с длиной


и дифференциальное уравнение (150) принимает вид

Перейдем к безразмерному времени


тогда

и дифференциальное уравнение (153) приобретает стандартную форму (151),
причем

Основное уравнение параметрических колебаний (151) называется уравнением Матье. Решения этого уравнения носят колебательный характер и главным образом зависят от конкретных значений параметров a и q. В одних случаях данной комбинации a и q соответствуют колебания, ограниченные по амплитуде, а в других - колебания с возрастающими амплитудами. Основную практическую важность представляет именно тенденция колебательного процесса: если амплитуды остаются ограниченными, то система устойчива; в противном случае имеет место параметрический резонанс, и система неустойчива.
Результаты решения уравнения Матье для двух различных комбинаций a и q показаны на рис.57 (эти решения получены при помощи электронного аналогового устройства). Хотя в обоих случаях параметр q системы одинаков (q = 0,1), колебания имеют совершенно разный характер из-за различия между значениями параметра a (a = 1; a = 1,2). В первом случае амплитуды возрастают, т.е. система неустойчива, а во втором случае остаются ограниченными, т.е. система устойчива.
Для практических целей наибольшее значение имеют границы между областями устойчивых и неустойчивых решений. Этот вопрос хорошо исследован, причем окончательные результаты представляются в виде диаграммы, построенной в плоскости параметров a и q, которая называется диаграммой Айнса-Стретта.
Каждой данной системе, характеризуемой параметрами a и q, соответствует точка с координатами a, q на диаграмме Айнса-Стретта (изображающая точка). Если изображающая точка находится в пределах заштрихованных полей диаграммы, то система устойчива; неустойчивым системам соответствуют изображающие точки, расположенные на белых полях.
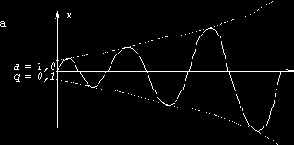
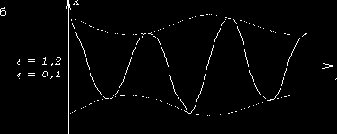
Рис. 57
На рис.58 показана часть диаграммы Айнса-Стретта, относящаяся к малым значениям параметра q. В качестве примера на диаграмме указаны точки 1 и 2, соответствующие параметрам a1 = 1; q1 = 0,1; a2 = 1,2; q2 = 0,1 (решения уравнения Матье для этих случаев даны на рис.57).

Рис. 58
Точка 1 находится в белой зоне (неустойчивость), и колебания происходят с возрастающими амплитудами (рис.57,а). Точка 2 находится в пределах заштрихованной зоны; ей отвечает движение с ограниченной амплитудой (рис.57,б).
В плоскости параметров a, q области устойчивости чередуются с областями неустойчивости, причем наиболее широкая, а потому и наиболее важная область неустойчивости содержит точку a = 1, q = 0. Диаграмма Айнса-Стретта полностью освобождает от выполнения каких-либо операций по решению уравнения Матье. Достаточно составить это уравнение, т.е. найти значения параметров системы a и q, после чего диаграмма дает ответ на вопрос об устойчивости или неустойчивости системы.
При возрастании частоты возбуждения параметры a и q уменьшаются. Так как отношение этих параметров остается постоянным, то последовательные состояния системы определяются изображающими точками на луче
