Общий случай

Способы решения. Если внешние силы изменяются по периодическому закону, то обычно их раскладывают в тригонометрический ряд, т.е. представляют в виде суммы гармоник. Затем на основании принципа независимости действия сил суммарное движение определяется как сумма движений, вызванных каждой из гармоник в отдельности. При таком подходе задача сводится к задаче о вынужденных колебаниях системы, вызываемых действием одной гармоники возмущения

 (или ), где амплитуда возмущающей силы, действующей по i-му направлению; частота возмущения, общая для всех сил, приложенных к различным точкам системы.

Решение этой основной задачи чаще всего ведут одним из двух способов: непосредственного решения или разложения по собственным формам колебаний. Наибольшее распространение в расчётной практике получил второй способ. Помимо этого, иногда используется способ разложения по собственным формам колебаний при сохранении заданного вида периодических нагрузок, т.е. без разложения их на гармонические составляющие.

Особенности каждого из этих способов рассмотрим на примере простейшей двухмассовой системы (рис.48).

 Непосредственное решение. Предполагая, что внешняя нагрузка разложена в тригонометрический ряд, исследуем движение системы, вызванное одной гармоникой возмущения. Силы, действующие на каждую массу, обозначим через

и . В дальнейшем будет рассмотрен также случай, когда обе силы имеют одинаковую частоту, но разные фазы.

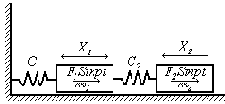
Рис. 48

Уравнения движения такой системы аналогичны уравнениям движения при свободных колебаниях, но нули в правых частях заменяются действующими силами

и :

                             (122)

Решение этой системы, как и решение одного уравнения, состоит из двух частей: решения соответствующей однородной системы и частного решения неоднородной системы (122).

Слагаемое, описывающее колебания с собственной частотой (т.е. решение однородной системы), меняется с течением времени, быстро уменьшаясь вследствие действия сил затухания. Основной интерес представляет вторая часть решения, соответствующая незатухающему стационарному процессу вынужденных колебаний.

Примем частное решение в виде

;  .                           (123)

После подстановки (123) в (122) получим два уравнения с двумя неизвестными амплитудами и :

                   (124)

Решая систему уравнений (124), находим

                           (125)

Знаменатели выражений для и  совпадают с левой частью частотного уравнения (42), если заменить в нём букву  буквой . Следовательно, если частота возмущения  совпадает с любой из двух собственных частот  или , то знаменатели формул (125) обратятся в нуль, а амплитуды  и  станут бесконечно большими (резонанс).

При  формулы (125) определяют статические отклонения обеих масс,  вызванные силами  и :



При  решения системы (125) стремятся к нулю. Зависимость амплитуды  от частоты показана на рис.49. Этот график построен для случая: . В этом случае число резонансов равно двум, что соответствует числу  степеней свободы системы и числу ее собственных частот.

 При помощи (125) можно найти форму вынужденных колебаний, определяемую отношением  к . В общем случае эта форма не совпадает ни с одной из собственных форм колебаний и только при резонансах форма вынужденных колебаний совпадает с формой свободных колебаний. Рассмотрим действие двух сил одинаковой частоты, но сдвинутых по фазе:  и .



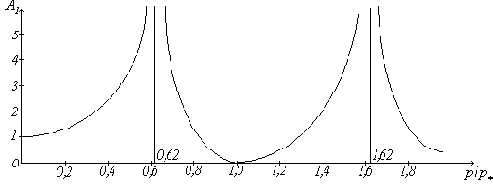
 Эти силы можно представить в виде



а затем решать две задачи: действуют только «синусные» составляющие  и ; действуют только «косинусные» составляющие  и .

В первой задаче получаются уравнения:



а во второй (когда частное решение имеет вид: ;  ):



Решая каждую из этих задач и суммируя результаты, получим решение исходной задачи.

Если возмущающие силы имеют полигармоническую структуру



то резонанс становится возможным при

;  ;  ;  ;

;  ;  ;  ,

т.е. при совпадении любой из частот возмущающей силы с любой из двух собственных частот системы.


Содержание раздела

---

---

---

Главная сайта

---