Крутильные колебания валов

Рассмотрим крутильные колебания многомассовой системы (рис. 26), которая является обще­принятой эквивалентной схемой для расчёта крутильных колебаний коленчатых валов. Колен­чатый вал приводится к эквивалентной схеме путём следующих замен: момент инерции заме­няющего диска относительно оси вала должен быть равен моменту инерции колена относи­тельно той же оси, при этом учитывается присоединённая масса шатуна; жёсткость на кручение участка заменяющего вала должна быть равна жёсткости на кручение соответствующего участка коленчатого вала.

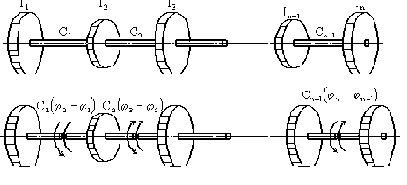
Рис. 26

Эти замены являются неплохой аппроксимацией, хотя и не обеспечивают полной эквивалент­ности обеих схем. Приведенный момент инерции масс колена и шатуна изменяется в процессе вращения коленчатого вала, поэтому замена колена диском с постоянным моментом инерции не является строгой. Кроме того, при действии на коленчатый вал двух противоположно направ­ленных пар деформация будет заключаться не только в закручивании участка между парами: вследствие изгиба произойдёт закручивание и других участков.

Тем не менее экспериментальные исследования подтверждают приемлемость эквивалентной схемы при достаточно тщательном определении эквивалентных моментов инерции и особенно эквивалентных жёсткостей.

Обозначим через

 моменты инерции масс дисков относительно продольной оси вала; - коэффициенты жёсткости участков при кручении; - углы по­воротов дисков вокруг продольной оси вала (рис. 26,а).

Крутильные моменты, действующие в сечениях вала, зависят от взаимного поворота двух смежных дисков и определяются формулами

на первом участке

;

на втором участке

;

на

- м участке

Уравнения движения удобнее всего составлять прямым способом (рис. 26,б).

                    (65)

Число этих уравнений

совпадает с числом дисков, т.е. с числом степеней свободы сис­темы.

Одним из решений системы (65) является

,                                          (66)

описывающее равномерное вращение вала и дисков как жёсткого целого.

Кроме того, возможно решение, описывающее упругие колебания системы

                                                 (67)

Подставляя (67) в (65), получим

           (68)

Система уравнений (68) содержит  неизвестных: n амплитуд и частоту колебаний .

Если преобразовать систему (68) и рассматривать её как однородную систему линейных ал­гебраических уравнений относительно неизвестных амплитуд , то ненулевое её решение можно получить, как это неоднократно делалось выше, из условия равенства нулю оп­ределителя. Раскрывая определитель, получим частотное уравнение.

Для иллюстрации сказанного запишем систему (68) в преобразованном виде при



Отсюда получим частотный определитель

                       (69)

и частотное уравнение

.                   (70)

В общем случае степень частотного уравнения относительно  равна n. Один из корней все­гда равен нулю и соответствует повороту всех дисков и вала как жёсткого целого. Остальные  корней (собственных частот) соответствуют упругим колебаниям.

При  решение частотного уравнения представляет значительные трудности. Но цепная структура уравнений (68) позволяет упростить определение собственных частот при помощи метода последовательных приближений (метода остатков). Суть метода состоит в следующем. Принимая  и  задаваясь ориентировочным значением , из первого уравнения системы (68) находят амплитуду ; из второго уравнения системы можно определить амплитуду , из третьего уравнения - амплитуду  и, наконец, из предпоследнего уравнения - амплитуду . Если в последнее уравнение системы (68) подставить вычисленные значения  и , то оно, вообще говоря, не будет удовлетворяться вследствие произвольности исходного значения  (которое, по сути, является первым приближением). Полученное значение левой части (остаток) характеризует меру неточности первого приближения  и одновременно показывает, в какую сторону нужно изменить расчётное значение  во втором приближении.

Далее производят повторный расчёт при новом значении . Знак и величина нового остатка помогут указать необходимую поправку в значении  для следующего приближения.


Расчёт повторяется до тех пор, пока не будет достигнут удовлетворительный результат в последнем уравнении.

При реализации метода удобнее всего использовать компактную табличную схему вычисле­ний, основанную на соотношениях типа

,                  (71)

которые получаются из уравнений (68) после сложения первых i уравнений системы. Соотно­шение (71) выражает равенство крутящего момента в сечении i-го участка вала (левая часть) сумме моментов сил инерции всех расположенных слева дисков (правая часть).

Задаваясь значением  и принимая , находим из соотношения (71) для :

.

Далее из того же соотношения для :

.

Общая формула имеет вид

.

Процесс продолжается таким образом до - го уравнения. После определения из него  можно переходить к последнему уравнению и вычислять его левую часть. Этот результат дол­жен быть равен нулю, так как если сложить все уравнения типа (71), то должно получиться

.

   Вследствие неточности принятого исходного значения  нуля в результате не получится. Ос­таток выражает неуравновешенный момент, который при точном выборе  должен быть равен нулю.

После нескольких расчётов такого типа (при разных значениях ) можно построить кривую зависимости остатка R от  (рис.27).



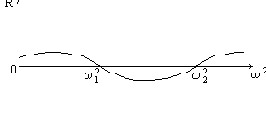
Рис. 27

Точки пересечения кривой с осью абсцисс соответствуют истинным значениям частот.

Объём вычислений может быть значительно уменьшен, если известны ориентировочные зна­чения частот, для определения которых часто используют замену заданной системы упрощён­ной трехмассовой системой.

При записи решения (67) предполагалось, что колебания являются одночастотными, т.е. для любого диска описываются одной гармоникой

.

Существование спектра частот  требует обобщения решения (67) и записи его в виде

   ,

где первый индекс у амплитуды означает номер диска, а второй индекс - номер соответствую­щей частоты.

Для получения общего решения необходимо также учесть возможность вращения всей сис­темы как жёсткого целого (что соответствует частоте ), т.е.


добавить слагаемое вида (66), и тогда общее решение уравнений движения (65)

 (72)

Уравнения (72) содержат 2n неизвестных:  неизвестных амплитуд колебаний первого диска ;  неизвестных начальных фаз ; угловое смеще­ние  и угловую скорость . Амплитуды колебаний всех остальных дисков  определяются через амплитуды составляющих колебаний первого диска ; отношения  зависят от но­мера частоты k и определяют соответствующие формы колебаний.

Таким образом, для полного решения задачи необходимо и достаточно указать 2n начальных условий - угловые смещения и угловые скорости всех n дисков.

При произвольно заданных начальных условиях колебания каждого диска будут многочастот­ными, т.е. будут представлять собой сумму гармоник. Если начальные условия смещения соот­ветствуют одной из собственных форм колебаний, то в дальнейшем процессе будут реализованы эта и только эта собственная форма и соответствующая собственная частота. В общем случае колебания будут носить сложный характер и представлять собой совокупность n форм колеба­ний. Относительное значение каждого из них зависит от близости заданной системы начальных смещений к той или иной собственной форме.


Содержание раздела

---

---