Кратные и нулевые корни частного уравнения

В некоторых случаях могут встречаться кратные корни частного уравнения, а в других случаях среди корней этого уравнения могут оказаться и нулевые.

Рассмотрим эти случаи на примере системы с двумя степенями свободы.

Из соответствующего такой системе частотного уравнения (39) следует, что при выполнении равенства

                  (49)

два корня частотного уравнения будут равны друг другу, а при выполнении равенства

                                                   (50)

один из корней частотного уравнения обращается в нуль.

В качестве примера рассмотрим свободные колебания плоской системы с двумя степенями свободы (рис.23).

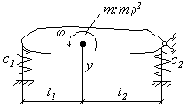
Рис. 23

Обозначим через

 и коэффициенты жёсткости пружин, а через m и  - массу и радиус инерции тела относительно оси, проходящей перпендикулярно плоскости чертежа через центр тяжести тела. За обобщённые координаты примем вертикальное перемещение центра тяжести  и угол поворота тела . Тогда кинетическая и потенциальная энергии имеют вид

 

После вычисления соответствующих производных уравнения

Лагранжа записываются так:

Предположим, что параметры рассматриваемой системы удовлетворяют двум простым (и практически реально осуществимым) соотношениям:

;   ,

тогда полученные дифференциальные уравнения принимают более простую форму

                                             (51)

   Следовательно, инерционные коэффициенты и обобщённые коэффициенты жёсткости в этих уравнениях

 

и условие (49) выполняется,  значит, рассматриваемая система имеет две одинаковые собст­венные частоты колебаний. Для выяснения этого можно было и не привлекать условие (49), так как из уравнений (51) непосредственно следует

.

Вследствие независимости уравнений (51) постоянные интегрирования одного уравнения не связаны с постоянными интегрирования другого уравнения

 

Для определения постоянных

 служат четыре начальных условия.

Рассмотрим пример системы с одной нулевой собственной частотой (рис.24).

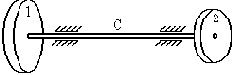
Рис. 24

Обозначим жёсткость вала на кручение через С; моменты инерции дисков относительно про­дольной оси системы - через

и .

Содержание раздела

---

---

---

Главная сайта

---