Теоретические основы динамики машин
          

Колебания в плоскости кольца


Рассмотрим круговой брус малой кривизны постоянного сечения с радиусом R осевой линии (рис.71,а). Будем считать груз нерастяжимым. Перемещение центра тяжести поперечного сечения, зафиксированного угловой координатой

, можно разложить на радиальный и окружной компоненты - соответственно
 и
. Из условия нерастяжимости оси бруса следует, что перемещения
 и
связаны зависимостью: 

                                

.                                                        (244)

а                                                                            б

         

                           

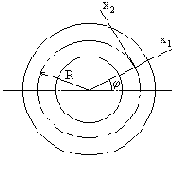
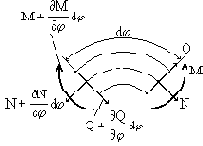
Рис. 71

Угол поворота поперечного сечения бруса в процессе движения определяется формулой

.                                             (245)

Изменение кривизны бруса

 равно производной от
 по дуге:

.                                        (246)

Изгибающий момент в поперечном сечении кольца:

.                                     (247)

Теперь составим уравнение движения элемента

 бруса (рис.71,б).

Помимо перечисленных сил, на элемент действует также сила инерции:



,

где

масса единицы длины бруса.

Проектируя приложенные к элементу силы на радиус, получим

.                                   (248)

Равенство нулю суммы проекций всех сил на направление касательной приводит к уравнению:

.                                      (249)

Уравнение моментов имеет вид

.                                                 (250)

Исключим из (248) и (249) нормальную силу N, а поперечную силу Q заменим её значением из (250):

.                         (251)

Подставляя сюда значение M из (247), получим уравнение движения в перемещениях

, и, наконец, исключая один из компонентов перемещения, с помощью условия нерастяжимости (244) придём к уравнению, в которое входит единственная переменная
:

.                (252)

Решение уравнения движения (252) будем искать в виде

;  
.

При этом для

 получается обыкновенное дифференциальное уравнение

,               (253)

.

Согласно общим правилам решения дифференциальных уравнений, следует найти общее решение уравнения (253), включающее шесть постоянных, и подчинить его граничным условиям.
На каждом конце бруса должны быть равны нулю либо компоненты перемещений

, либо соответствующие им внутренние силы. Равенство нулю определителя системы, выражающей граничные условия, приводит к частотному уравнению.

Для замкнутого кольца граничные условия заменяются условиями периодичности, которые выполняются, если принять

;  
.                                (254)

Подставляя (254) в (253), устанавливаем, что последнее удовлетворяется тождественно, если

.                                (255)

Формула (255) определяет частоты собственных колебаний кольца в своей плоскости. Значению
 соответствует нулевая частота, так как при
 формулы (254) описывают смещение кольца как жёсткого тела.


Содержание раздела



Главная сайта