Колебания, перпендикулярные плоскости кольца

В этом случае положение поперечного сечения кольца в процессе движения характеризуется смещением

его центра тяжести из плоскости кольца и углом поворота сечения х4 (рис.72,а). В поперечном сечении кольца возникают изгибающие и крутящие моменты (рис.72,б), а также поперечная сила, перпендикулярная плоскости кольца.

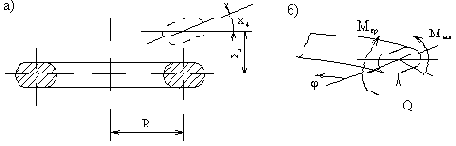
Рис. 72

Установим зависимость моментов от перемещений. Так как задача линейная, то рассмотрим сначала силовые факторы, связанные со смещением х3, а затем - с х4.

Если х3 постоянно по длине окружности, то кольцо смещается как жёсткое целое, и внутренние силы не возникнут. Если х3 изменяется в зависимости от центрального угла по линейному закону

, то ось бруса превращается в винтовую линию, т.е. брус деформируется подобно витку пружины при растяжении. Известно, что в этом случае в поперечных сечениях возникает крутящий момент

где GJкр- крутильная жёсткость бруса.

Если при этом отлична от нуля и вторая производная

, то

меняется кривизна бруса и возникает изгибающий момент

где J1 - момент инерции сечения относительно центральной оси, лежащей в плоскости кривизны.

Найдём силовые факторы, связанные с поворотом х4. Если х4 постоянно, то происходит осесимметричный изгиб кольца, причём в его сечениях возникает изгибающий момент

При переменном по длине повороте х4 соседние сечения поворачиваются друг относительно друга и возникает крутящий момент

Суммируя силовые факторы, связанные с перемещениями х3 и х4, ,получаем

(256)

Составим уравнение движения элемента Rd

бруса (рис.73).

Будем пренебрегать инерцией поворота элемента вокруг своей оси.

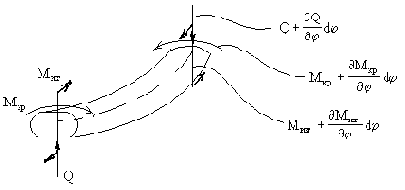
Рис. 73

Условие динамического равновесия в направлении нормали к плоскости кольца приводит к уравнению:

. (257)

Сумма моментов относительно нормали к оси элемента:

. (258)

Сумма моментов относительно касательной к оси элемента:

. (259)

Исключая поперечную силу из (257) и (258) и заменяя моменты в полученном уравнении и уравнении (259) их значениями (256), приходим к системе уравнений, в которую входят только перемещения х3 и х4:

(260)

Ограничиваясь исследованием собственных колебаний замкнутого

кольца, решение уравнений (260) можно представить в виде

x3 =Acoskj×coswt , x4 = Bcoskj×coswt . (261)

Подставляя значения (261) в уравнение движения (260), получим

(262)

Из равенства нулю определителя этой системы получим частотное уравнение, корни которого - собственные частоты - таковы:

(263)

Наименьшая отличная от нуля частота соответствует k=2.

Содержание раздела

Главная сайта