Фрикционные автоколебания

Особого внимания заслуживают механические автоколебания, возникающие в системах с трением. Сила трения, которая в ранее рассмотренных примерах оказывалась причиной затухания колебаний, может явиться причиной их раскачивания.

Рассмотрим простейшую систему (рис.62,а), состоящую из двух вращающихся барабанов и бесконечной ленты.

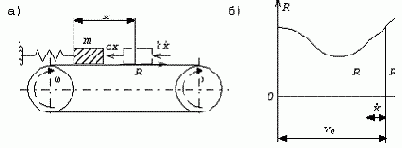
Рис. 62

На ленте лежит груз массой

, движение которого ограничено пружиной с жесткостью с. Развивающаяся при скольжении груза сила трения смещает груз вправо и вызывает некоторое удлинение пружины. Пусть в положении равновесия груза сила трения равна R0, тогда статическое смещение груза

(161)

Для дальнейших рассуждений необходимо учесть, что сила трения R зависит от относительной скорости движения V (при заданном нормальном давлении груза, которое будем считать постоянным). Пусть характеристика трения имеет вид, показанный на рис.62,б, где значения V0 и R0 соответствуют состоянию равновесия груза.

Положим, что вследствие какого-либо возмущения в мгновение t=0 груз выведен из состояния покоя. Выясним характер движения, которое возникает после такого возмущения, считая, что скорость движения ленты в процессе колебаний груза не изменяется. Пусть в текущее мгновение

смещение груза равно

, его скорость равна

, а скорость скольжения

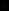
В это мгновение на груз действуют три силы: сила трения R, реакция пружины

и внешнее сопротивление, которое будем считать пропорциональным скорости и равным

Сила

отличается от силы

, поскольку скорость относительного движения

отличается от скорости

. При малых колебаниях относительной скорости можно принять:

, (162)

где

- тангенс угла наклона характеристики трения в точке с координатами

Уравнение движения груза:

Подставляя сюда (162), получим

или

(163)

Сместим начало отсчета перемещений в точку

, т.е. введем новую переменную

Тогда (163) имеет вид

Согласно (161), сумма двух последних слагаемых равна нулю, поэтому получим уравнение

(164)

Анализ структуры этого уравнения показывает, что с увеличением времени колебания должны исчезать, если сумма

положительна. Это обязательно имеет место на восходящем участке характеристики трения, где

.

Однако при небольших значениях

(нисходящий участок характеристики трения) величина

становятся отрицательной. Если при этом

, то сумма

остается положительной, и колебания будут затухающими. Если сумма

обращается в нуль, т.е.

, то в уравнении (164) исчезает член, соответствующий затуханию, и становятся возможными колебания с постоянной амплитудой. Если же сумма

отрицательна, то система обладает как бы «отрицательным затуханием», и колебания с течением времени будут возрастать за счет энергии, передаваемой движущейся лентой.

Природу «отрицательного затухания» при падающей характеристике трения можно выяснить исходя из следующих рассуждений. Когда груз движется вправо, т.е. по ходу движения ленты, относительная скорость скольжения уменьшается; вместе с этим сила трения увеличивается и ее приращение направлено вправо, т.е. также в сторону движения. В другом интервале движения, когда груз движется влево, приращение силы трения направлено также влево, т.е. опять в сторону движения. Такой характер изменения силы трения и является причиной возрастания колебаний.

Итак, для возрастания колебаний необходимо выполнение условия:

, что возможно только при достаточной крутизне падения характеристики трения. Обычно указанное условие выполняется лишь при малой скорости

.

При помощи тех же рассуждений можно прийти к выводу о возможности автоколебаний упруго закрепленной колодки, прижатой к вращающемуся диску (рис.63,а), а также груза на пружине, когда левому ее концу задано движение с постоянной скоростью (рис.63,б). В обоих этих случаях необходимым условием автоколебаний также является наличие нисходящего участка характеристики трения.

К этому же классу явлений относятся автоколебания, возникающие при резании металлов на станках. Рассмотрим природу этих автоколебаний.

Со стороны заготовки на резец действует реакция

, которая может быть разложена на составляющие

(рис.63,в,г). Резец упруго закреплен и его конец может совершать колебания как в горизонтальном, так и в вертикальном направлениях. Для выявления возможности автоколебаний достаточно рассмотреть колебания только в горизонтальном направлении

и учесть важный экспериментальный результат: горизонтальная составляющая

зависит от скорости горизонтальных колебаний резца

.

На резец действуют три силы: сила упругости - су системы резец-суппорт (где с - коэффициент жесткости); реакция заготовки

и сумма различных неупругих сопротивлений, которая может быть объединена в одно слагаемое вида

Рис. 63

Таким образом, уравнение движения системы резец-суппорт имеет вид

где

- приведенная масса системы резец-суппорт.

После линеаризации силы

, согласно (162), вновь приходим к уравнению типа (164), следовательно, и в этом случае автоколебания возможны, если характеристика силы

- нисходящая.

Как установлено, неустойчивость состояния равновесия может быть обнаружена в предположении малости колебаний, т.е. при помощи линейного приближения. Однако, если отказаться от этого предположения и проследить за дальнейшим течением процесса, то обнаруживается, что рост амплитуд постепенно замедляется и в конечном итоге амплитуда полностью стабилизируется. Этот процесс установившихся (стационарных) автоколебаний (рис.64) называется предельным циклом.

Важной особенностью предельного цикла является его полная независимость от начальных условий; после любого возмущения состояния равновесия система приближается к одному и тому же предельному циклу.

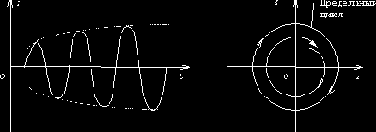
Рис. 64

Для выявления параметров (частоты, амплитуды) установившихся автоколебаний необходим анализ соответствующей нелинейной задачи.

В некоторых случаях стационарные автоколебания носят почти гармонический характер и совершаются с частотой свободных колебаний системы; соответствующие системы называются квазилинейными. В других случаях стационарные автоколебания резко отличаются от гармонических, сопровождаются остановками и скачками скорости; такие автоколебания и соответствующие системы называются релаксационными или разрывными.

Содержание раздела