Флаттер крыла в воздушном потоке
Как уже говорилось выше, флаттером называются автоколебания тел в потоке газа или жидкости.
При появлении первых скоростных самолетов флаттер служил причиной многочисленных катастроф. Явление флаттера тесно связано с теми воздействиями, которые поток воздуха оказывает на колеблющееся крыло.
Ограничимся рассмотрением принципиальной картины этого явления. При флаттере крыло самолета совершает изгибно-крутильные колебания, поэтому для анализа этого явления необходимо учесть по крайней мере две степени свободы крыла. При практических расчетах достаточно учесть движения крыла по первым формам собственных изгибных и крутильных колебаний. В еще более простом варианте расчета рассмотрим жесткое крыло, имеющее две степени свободы, соответствующие его вертикальному перемещению и повороту (рис.65).
Существенное значение имеет положение центра тяжести крыла, т.е. той точки его хорды, приложение вертикальной силы в которой вызывает только вертикальное перемещение крыла, но не его поворот. К этой точке (точка 0 на рис.65) будем приводить действующие на крыло силы.
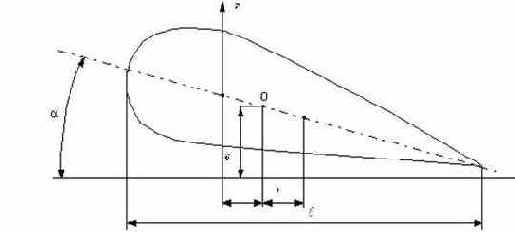
Рис. 65
Если обозначить вертикальное перемещение центра жесткости крыла через






Сила инерции и момент сил инерции относительно точки 0 составляют соответственно

где



Наибольшие трудности представляет определение изменений аэродинамических сил, возникающих вследствие движения крыла. Простейшая гипотеза относительно этих сил состоит в том, что их можно вычислить так же, как и при неподвижном крыле, подставив в соответствующие формулы значения мгновенного угла атаки. В этом предположении получаем увеличение подъемной силы и момента

где




Формулы (166) представляют собой грубое приближение, так как в них полностью игнорируется влияние движения крыла на обтекание. Более точное решение задачи показывает, что если крыло совершает, например, гармонические колебания с частотой

Как величина присоединенной массы, так и фазовый сдвиг зависят от безразмерного параметра

Ради упрощения расчета не будем учитывать всех этих обстоятельств и дополнительно в первой из формул (166) пренебрежем слагаемым


где

Решение системы (167) отыщем в виде, соответствующем гармоническим колебаниям:

Подставляя (168) в (167), получим систему однородных алгебраических уравнений относительно



Приравнивая нулю определитель системы (169), получим частотное уравнение. Для того чтобы привести это уравнение к более простому виду, введем следующие обозначения:

- собственные частоты поступательных (изгибных) и крутильных колебаний крыла;

- относительная плотность крыла.
Тогда частотное уравнение можно представить в так:

При нулевой скорости потока V=0 это уравнение даёт два положительных значения W2, соответствующих двум собственным частотам системы.
С увеличением скорости потока возможно появление двух типов неустойчивости. Так, один из корней уравнения (170) может обратиться в нуль, что соответствует обращению в нуль свободного члена уравнения (170):

Обращение в нуль частоты собственных колебаний системы свидетельствует о её статической неустойчивости. Действительно, возвращаясь в формуле (171) к первоначальным обозначениям, приведём её к виду

Если это соотношение выполняется, то при повороте крыла на угол а момент дополнительной подъёмной силы

уравновешивается упругим моментом

Явление статической потери устойчивости крыла при достижении скоростью потока значения Vg называется дивергенцией.
Для крыльев самолётов, как правило, скорость дивергенции существенно превышает скорость полета и дивергенция не представляет реальной опасности.
Другой вид потери устойчивости – изгибно-крутильный флаттер - связан с тем, что частоты, определяемые из (170), становятся комплексными числами. Если имеются сопряжённые комплексные частоты


Экспоненциальные множители с действительными положительными показателями неограниченно возрастают.
Таким образом, в этом случае движение представляет собой колебания с нарастающими амплитудами (колебательный характер движения определяется множителями

Итак, условием наступления флаттера является появление комплексных корней уравнения (170), что происходит при обращении в нуль (назовём это «граничным условием») его дискриминанта:

Из уравнения (172) легко вычислить скорость флаттера.
Проследим на числовом примере характер изменения частоты свободных колебаний крыла по уравнению (170) при увеличении скорости потока.
Допустим, что





Этим данным соответствуют скорость дивергенции, вычисленная по уравнению (171),


График изменения частот колебаний системы в зависимости от скорости потока, построенный в соответствии с уравнением (170),показан на рис.66.
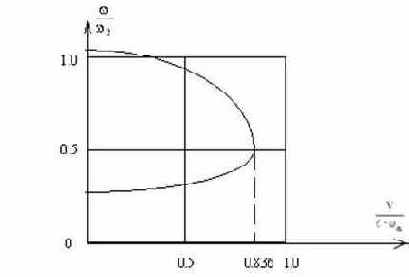
Рис. 66
При V=0 система имеет две частоты собственных колебаний, мало отличающиеся от частот чисто крутильных и чисто изгибных колебаний. С увеличением скорости потока частоты сближаются, и при скорости флаттера оказываются равными друг другу.
Наличие кратных собственных частот для консервативной системы не связано с какими-либо особенностями её поведения.Для неконсервативной системы, которую представляет собой крыло, находящееся в потоке воздуха, слияние двух частот ведёт к потере устойчивости движения. В процессе колебаний система начинает интенсивно потреблять энергию потока и амплитуды колебаний неограниченно возрастают. Механизм этого явления легко понять, если представить себе, что происходящие с одинаковой частотой крутильные и изгибные колебания крыла сдвинуты по фазе на
