Действие произвольной периодической

В практических приложениях часто встречаются периодические возмущающие силы более сложного характера, чем рассмотренные выше.

Так, на рис.44,а показан закон изменения крутящего момента, создаваемого четырёхтактным двигателем внутреннего сгорания. Другой пример – периодические "безмассовые" удары – показан на рис.44,б.

Силы (моменты) рассматриваемого вида имеют чётко выраженный период колебаний Т, но не описываются единым аналитическим выражением. В подобных случаях чаще всего пользуются разложением периодической нагрузки в ряд Фурье. При этом сила представляется в виде суммы гармонических составляющих, а затем определяется эффект, вызываемый каждой из составляющих; после этого полученные частные эффекты суммируются.

Периодическую силу F(t) можно представить в виде ряда Фурье:

где

- основная частота возмущения.

Коэффициенты

вычисляются по формулам

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

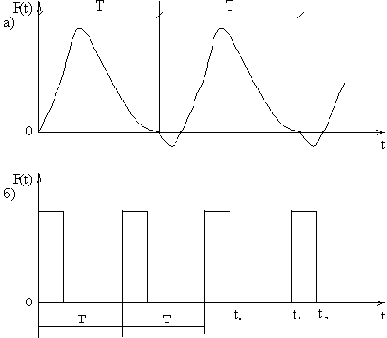
Рис. 44

Опираясь на решение (98), полученное для одной гармоники, находим

(103)

Это решение состоит из постоянного слагаемого

, соответствующего среднему значению возмущающей силы, и ряда, соответствующего гармоническим колебаниям с частотами p, 2p, .... Если собственная частота совпадает с частотой какой-либо одной гармоники np (n=1,2,...), то соответствующее слагаемое в (103) стремится к бесконечности. Следовательно, в общем случае периодической возмущающей силы резонанс наступает не только тогда, когда собственная частота

равна основной частоте возмущающей силы p, но и когда

кратно p (в некоторых частных случаях в (103) пропадают некоторые слагаемые, и резонанс наступает не при любой кратности).

Рассмотренный способ чётко выявляет условия наступления резонанса. Недостатком этого способа является сложность вычислений, необходимых для учёта большого числа слагаемых в (103). Так, возмущающую силу, показанную на рис.44,a, для достаточной точности необходимо заменить примерно десятью гармониками.

Содержание раздела

Главная сайта