Действие непериодической возмущающей силы

1. Действие линейно возрастающей силы (рис.38,а)

Используем выражение (91), полагая

График этого движения показан на рис.38,б.

Рис. 38

Перемещения нарастают по сложному закону, представляющему собой сумму синусоиды и линейной функции. Дополнительное синусоидальное колебание тем существеннее, чем быстрее нарастает сила F, т.е. чем больше а.

Колебания подрессоренного груза при движении по неровной дороге (рис.39)

Пусть профиль дороги задан уравнением

=h(1-),

где h - предел, к которому стремится высота профиля;

- параметр, характеризующий кривизну профиля.

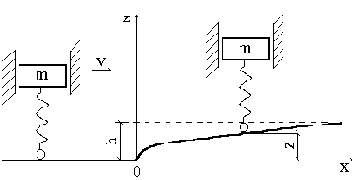
Рис. 39

Обозначим  через V скорость движения груза массой m и примем начало отсчёта времени в мгновение, когда опорная точка проходит начало неровности. Тогда х=Vt и движение опорной точки по вертикали определяется законом

).

Дифференцируя, находим

.

На основании  (92) получим закон движения груза по вертикали:

Z=f(t)-

.

Так как важным является не абсолютное изменение положения груза, а его колебания относительно опорной точки, то рассмотрим разность, определяющую дополнительную деформацию пружины

.

Интегрируя, находим

,

где

 определяется соотношением

.

Отсюда следует, что при весьма малой скорости параметр

  стремится к , а разность z-f - к нулю. Наоборот, при весьма большой скорости (а также при весьма большом значении параметра ) параметр стремится к нулю, и колебания приближённо описываются законом

2. Действие медленно изменяющихся сил

Рассмотрим полученное выше решение задачи о вынужденных колебаниях (91). Первое слагаемое представляет собой статическое отклонение, вызванное силой F(t). Второе слагаемое - это поправка к статическому отклонению, причём эта поправка зависит от скорости изменения силы

.

При малой скорости нарастания внешней нагрузки динамическая поправка к статическому решению относительно мала и нагружение практически можно рассматривать как статическое.

А.Н.Крылов дал оценку динамической поправки для общего случая возмущающей силы. Если кривая F(t) имеет один максимум (рис.40,а), то, обозначая максимальное значение

 через (рис.40,б), имеем

.

Произведение     представляет собой максимально возможное приращение возмущающей силы за промежуток времени, равный полупериоду свободных колебаний; обозначая это произведение через Fmax, получим

.



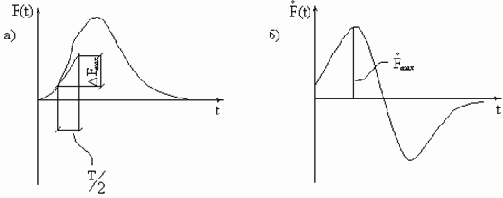
Рис. 40

Если сила возрастает равномерно в течение времени t0, то  и динамическая "добавка" составляет

.

Её относительная величина

.

Отсюда следует, что если период свободных колебаний мал по сравнению с продолжительностью действия силы, то она может считаться медленно изменяющейся, а  её действие можно рассчитывать без учёта динамичности, т.е. считать силу приложенной статически.

3. Действие быстро исчезающих сил

Пусть возмущающая нагрузка действует в течение весьма короткого промежутка времени. Даже значительная нагрузка может оказаться  безопасной, если длительность её действия мала по сравнению с периодом свободных колебаний системы.

Рассмотрим действие силы F, которая внезапно прикладывается в момент времени t=0, действует в течение некоторого промежутка времени а, а затем также внезапно исчезает. Можно показать, что если a<

, то максимальное отклонение системы достигается после исчезновения силы. В таком случае для t>à, согласно решению (89), имеем

                                .                 (93)

Обозначим отношение промежутка времени а к периоду свободных колебаний Т через , тогда

.

Максимальное отклонение  в соответствии с (93):

.

Следовательно, динамический коэффициент:



Значения динамического коэффициента при действии силы малой продолжительности приведены в табл. 5.

                                                                                                 Таблица 5

	0	0,01	0,02	0,03	0,05	0,10	0,15	0,25	0,5
	0	0,062	0,126	0,188	0,313	0,618	0,908	1,413	2,000

Из приведенной таблицы видно, что если сила действует в течение малой доли периода свободных колебаний, то эффект такой кратковременной силы во много раз меньше статического. Аналогичный вывод можно сделать и в случае, когда возмущающая сила представляет собой одну половину синусоиды.



Покажем, что действие кратковременной силы приближённо можно оценить её импульсом. Для t>à решение имеет вид

,

или

=

=.

Но так как отношение   меньше отношения, то  есть малое число.

Тогда приближённо можно записать

.

Входящий сюда интеграл есть импульс силы F(t), т.е. движение системы определяется величиной импульса кратковременной силы, причём подробности изменения силы за промежуток времени а не играют роли.


Содержание раздела

---

---