Действие гармонической силы

Случай, когда возмущающая сила изменяется по гармоническому закону

F=F0  sin pt,                                            (94)

где  F0 - амплитуда силы; p - её частота, является наиболее распространённым в практике.

Описание колебательного процесса, вызываемого такой силой, при нулевых начальных условиях можно получить при помощи  (89)

.                                   (95)

Вычисляя интеграл, при

  находим                   

.                              (96)

Заменим

 и обозначим  (прогиб, вызванный статически приложенной постоянной силой F0 ), тогда

.                                (97)

Из (97) следует, что при нулевых начальных условиях возникают сложные колебания, состоящие из двух частей: колебаний, происходящих с частотой p возмущающей силы, и колебаний, происходящих с собственной частотой

. Обычно первые колебания называют вынужденными, а вторые - свободными. Такая терминология является условной. Дело в том, что и вторые колебания вызваны действующей возмущающей силой, и их амплитуда зависит от этой силы; в этом смысле вторые колебания также являются вынужденными. Указанные наименования получили широкое распространение потому, что первое слагаемое имеет частоту возмущающей силы, а второе меняется с собственной частотой системы.

Составляющая, названная выше свободными колебаниями, быстро исчезает, поэтому достаточно ограничиться изучением стационарной, незатухающей части решения

 .                                            (98)

Амплитуда вынужденных колебаний

                                                 (99)

отличается от прогиба

, подсчитанного в предположении статического действия силы F0. Отношение  можно назвать динамическим коэффициентом

 .                                                (100)

Динамический коэффициент

 зависит только от отношения частот . На рис.41,a приведена кривая зависимости от отношения .

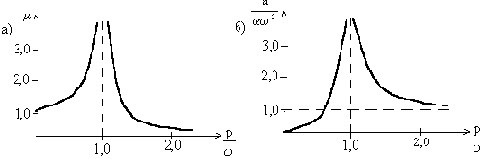
Рис.  41

При малой частоте возмущающей силы динамический коэффициент близок к единице. С ростом частоты p динамический коэффициент быстро увеличивается и при

 обращается в бесконечность.
Это соответствует состоянию резонанса, когда амплитуда вынужденных колебаний стремится к бесконечности (если учесть силы неупругого сопротивления, то амплитуда при резонансе окажется хотя и ограниченной, но обычно настолько значительной, что состояние резонанса всё равно следует считать опасным).

   Если частота p больше собственной частоты  , то амплитуды становятся конечными; при  динамический коэффициент становится меньше единицы, т.е. динамический эффект слабее соответствующего статического эффекта. При очень больших значениях отношения  динамический коэффициент становится весьма малым. Это означает, что сила высокой частоты не вызывает ощутимых колебаний в упругой низкочастотной системе, которая как бы "не успевает" отзываться на быстрые изменения возмущающей силы.

В приведенных рассуждениях считалось, что амплитудное значение возмущающей силы не связано с её частотой. Однако чаще бывает обратное, например, при вращении неуравновешенного ротора на опоры передаётся возмущающая сила

,

где - масса ротора; e- её эксцентриситет; - угловая скорость.

В данном случае амплитуда возмущающей силы пропорциональна квадрату , и вместо решения (96) при  следует принимать

.

Амплитуда стационарных колебаний при этом определяется выражением

,

в котором параметр системы  не зависит от частоты p.

На рис.41,б представлено изменение амплитуды колебаний в зависимости от отношения .

Как видно, при  имеет место резонанс, а при p» амплитуда стремится к значению .

Остановимся подробнее на случае совпадения частот (резонанс).



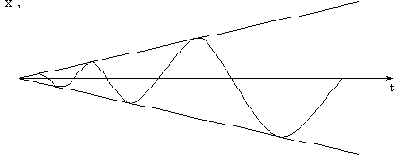
Рис. 42

При этом интеграл (95) принимает вид

.

После вычисления получим

.

График этого движения показан на рис.42. Как видно, при совпадении частот амплитуда нарастает по линейному закону и за конечный промежуток времени не обращается в бесконечность. Из этого вытекает принципиальная возможность перехода через резонанс, так как  в процессе разгона двигателей равенство  выполняется лишь одно мгновение и амплитуды при переходе могут не достигнуть опасных величин.


Содержание раздела

---

---