Точный останов электропривода
Рассмотрим задачу точного позиционирования рабочего органа механизма в заданных точках пути по сигналам путевых датчиков, или, как ее называют иначе, задачу автоматического точного останова электропривода. Эта задача сводится к автоматическому отключению двигателя и наложению механического тормоза в такой точке пути, из которой электропривод за время торможения, двигаясь по инерции, перемещается в заданную точку пути с требуемой точностью. Процесс останова, таким образом, начинается с поступления в схему управления электроприводом импульса путевого командоаппарата на отключение двигателя и наложение механического тормоза. Если принять, что отключение двигателя и наложение механического тормоза происходят одновременно и усилие тормоза возрастает до установленного значения скачком, то весь процесс точного останова можно разделить на два этапа.
Первый этап обусловлен наличием собственного времени срабатывания аппаратуры ta в схеме управления электроприводом. Вследствие возникающего запаздывания в течение времени ta двигатель не отключается от сети, и электропривод продолжает движение со скоростью wнач, с которой он подошел к датчику точного останова, и проходит путь
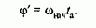
По истечении времени срабатывания аппаратуры двигатель отключается от сети, и накладывается механический тормоз. Наступает второй этап процесса останова, во время которого запасенная во всех движущихся массах системы кинетическая энергия расходуется на совершение работы по преодолению сил статического сопротивления движению на проходимом при этом пути ф":
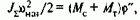
где Мт - момент механического тормоза. Откуда

На первом этапе скорость w=wнач=const, на втором она изменяется в зависимости от пути по закону
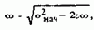
где e=(Мс+МТ)/JS- ускорение электропривода на втором этапе.
Зависимость w=f(ф) при установке датчика точного останова (ДТО) в точке ф=0 и некоторой начальной скорости wнач
показана на рис.9.1 (кривая 1). Так как все параметры, определяющие по (9.1) путь, проходимый электроприводом в процессе точного останова, при работе электропривода не остаются постоянными, абсолютно точный останов невозможен.
Так как после срабатывания ДТО движение системы является неуправляемым,наибольшая неточность останова зависит только от пределов изменения параметров, входящих в (9.1). Эти пределы можно характеризовать следующими выражениями, представляющими наибольшие и наименьшие значения соответствующих переменных и параметров:

где wср, tср, JSср, Мсср, Мтср и eср - средние значения параметров; Dw, Dt, DJ, DМс, DМТ и Demax - отклонения от средних значений параметров.

f=fcp±Dfmax (9.3)
где ф - средний путь при точном останове; Dфmax- максимальная ошибка позиционирования или максимальная неточность останова.
Как показано на рис.9.1, ДТО должен устанавливаться на расстоянии ф3=фcp , там же кривые 2 и 3 дают представления о зависимостях w=f(ф) при сочетаниях параметров, соответствующих наибольшей ошибке позиционирования.

С помощью (9.2) можно определить по (9.1) наибольший путь при точном останове

и его наименьшее значение
причем в (9.4) и (9.5) обозначено Мдин.ср=Мс.ср+Мт.ср и ВМДИН.max=DМс.max+DМТ.max. Эти выражения позволяют получить среднее значение пути, проходимого электроприводом в процессе точного останова:


Максимальная неточность останова


Анализ (9.7) свидетельствует о том, что максимальная неточность останова тем больше, чем больше средний путь при останове и чем больше относительные отклонения всех факторов, от которых он зависит, от соответствующих средних значений. Так как относительные отклонения в (9.6) и (9.7) значительно меньше единицы, то можно пренебречь их произведениями и квадратами, при этом (9.7) можно с некоторым ущербом для точности представить в значительно более удобном для пользования виде:
 |
Выражение (9.8) показывает, что наиболее существенно ошибка позиционирования зависит от средней начальной скорости и от ее отклонений от среднего значения. Поэтому из (9.8) следует, что основным фактором, вызывающим неточность останова, являются изменения нагрузки электропривода, так как они непосредственно сказываются на значении динамического момента Мдин и при данной жесткости механической характеристики электропривода определяют основное отклонение начальной скорости от среднего значения, обусловленное изменениями нагрузки, Dwmax=DМсmax/b.
Изменения нагрузки в большинстве случаев связаны с одновременным изменением суммарного приведенного момента инерции электропривода JS При данных пределах изменения статической нагрузки и известных tcp и Dtmax основным средством уменьшения ошибки позиционирования является снижение средней скорости электропривода при подходе к ДТО и увеличение жесткости механической характеристики, соответствующей работе двигателя с этой пониженной скоростью. Для получения формулы, связывающей требуемую среднюю пониженную скорость и жесткость механической характеристики с допустимой неточностью останова, примем в (9.8)
Dfmax=Dfmax.доп
где Dfmax.доп – жопустимая ошибка позиционирования, определяемая технологическими требованиями к электроприводу. При этом получается квадратное уравнение

решение которого дает следующее выражение для допустимой средней остановочной скорости:

где

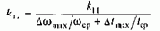


|
Рис.9.2. Механические характеристики, обеспечивающие требуемую точность позиционирования |
Рис.9.3. Зависимости w=f(ф) в процессе замедления до пониженной корости и точного останова электропривода |
Таким образом, рассматриваемый способ управления положением может обеспечить любую требуемую точность останова рабочего органа механизма в заданные позиции при правильном выборе средней остановочной скорости w и обеспечении высокой точности стабилизации этой скорости. Это означает, что требование автоматического точного останова электропривода определяет необходимый диапазон регулирования скорости электропривода D=wном/wср при заданных пределах изменения нагрузки и других возмущающих факторов.
Важным достоинством рассматриваемого способа является простота реализации, однако при высоких требованиях к точности останова и большом диапазоне регулирования, требуемом для получения этой точности, процесс точного позиционирования может при определенных условиях недопустимо затягиваться и снижать производительность позиционного механизма.
Указанные условия определяются динамическими свойствами электропривода в процессе замедления электропривода от рабочей скорости wном до пониженной остановочной скорости wср.
На рис.9.3 показаны зависимости w=f(f) при двух нагрузках электропривода Мс=Мс.max и Мс=Мс.min, соответствующие как процессу точного останова, так и предшествующему процессу замедления.
Кривые построены в предположении, что при любой нагрузке процессы замедления протекают при неизменном тормозном моменте двигателя М=Мmax=const. Тогда ускорение электропривода в этом процессе будет зависеть от нагрузки:
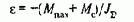
причем наименьшей нагрузке на валу Мс.min соответствует и наименьшее по абсолютному значению ускорение. При Мс=Мс.min начальная рабочая скорость при ограниченной жесткости механических характеристик электропривода максимальна: wр=wр.max, путь, проходимый электроприводом за время снижения скорости от wр.max до wнач.max при минимальном ускорении emin, также имеет максимальное значение fзам.max. Датчик импульса замедления (ДИЗ), дающий команду на замедление, устанавливается от ДТО на расстоянии 1,1·фзам.max, поэтому, как показано на рис.9.3, при Мс=Мс.min электропривод на пониженной скорости wнач.max проходит весьма небольшой отрезок пути и время дотягивания к ДТО невелико. При М=Мс.max, wр=wр.min соответственно fзам=fзам.min<<1,1фзам.max Как следствие большой отрезок пути Dфзам=1,1фзам.max-фзам.max электропривод проходит на пониженной скорости wнач.min, время дотягивания при wнач.min<<wр.min оказывается значительным и соизмеримым с общим временем, требующимся для перемещения механизма из исходного рабочего положения в заданное.
Рассматривая рис.9.3, можно заключить, что время дотягивания при любых нагрузках может быть сведено к минимуму, если устранить статическую ошибку регулирования скорости и сформировать стабильную зависимость w=f(t) в процессе замедления, инвариантную относительно нагрузки.Поэтому при большом диапазоне регулирования скорости, требуемом по условиям точного останова, возникает необходимость использования замкнутых систем регулирования скорости в системе УП-Д с достаточно высокими показателями качества и точности регулирования как в статических, так и в динамических режимах.
Однако даже при применении этой совершенной системы, с точки зрения регулирования положения, электропривод при рассмотренном способе точного позиционирования ведет себя как разомкнутая система, в которой изменения всех факторов, влияющих на путь, проходимый при точном останове, непосредственно сказываются на достигаемой точности, а небольшая нестабильность кривой изменения скорости при замедлении может существенно уменьшать быстродействие. Поэтому в наиболее сложных случаях электроприводы позиционных механизмов по системе УП-Д включаются в замкнутую систему автоматического регулирования положения по отклонению.