Статические характеристики и динамические
В связи с развитием регулируемого асинхронного электропривода с частотным управлением значительный практический интерес представляет изучение свойств асинхронного электромеханического преобразователя при питании от источника тока. Это обусловлено тем, что значительная часть используемых преобразователей частоты обладает свойствами источника тока, т. е. формирует в фазах двигателя токи, которые не зависят от режима работы и параметров двигателя, а определяются только сигналом задания. Схема включения двигателя для этого случая показана на рис.3.39. В этой схеме двигатель получает питание от трехфазного источника тока. Значение тока определяется напряжением задания тока мзт, а частота - напряжением мзч.

Так как в схеме рис.3.39 обмотки статора питаются неизменным током, уравнения механической характеристики (3.64) запишутся в виде

потокосцепления в (3.97) могут быть выражены через токи:

Подставив в уравнение для обмотки 2х выражения потокосцеплений (3.98), определим ток фазы 2у.

где
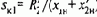
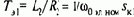
Система (3.97) нелинейна, поэтому при преобразованиях необходимо соблюдать условия, отмеченные в §3.12. Подставим (3.99) в уравнение для обмотки 2у и с соблюдением указанных условий преобразований разрешим его относительно тока фазы 2х:

Искомое уравнение механической характеристики асинхронного электромеханического преобразователя при питании от источника тока получим, подставив (3.100) в последнее уравнение системы (3.97)

здесь Мк1 - критический момент при питании от источника тока. В переменных двухфазной модели он получен в виде

Уравнение критического момента для трехфазной машины получим, заменив максимальное значение тока двухфазной модели I1max действующим значением тока фазы трехфазного двигателя I1 с помощью формулы (2.37):
Кривая намагничивания представлена на рис.3.41,б, там же построена кривая х=f(I), соответствующая данной кривой намагничивания. Для анализа формы статических характеристик с приближенным учетом насыщения характеристика Фm=f(Im) аппроксимирована двумя прямыми. При Im<Imнас магнитная цепь машины ненасыщена и xm=xmн=const (прямая 1). Если Im>Imнас, насыщение сказывается существенно и приближенно можно принять Фm=Фцнас=const (прямая 2 на рис.3.41,б).
Так как Im<I1 то при Im<Imнас магнитная цепь двигателя при любых скольжениях не насыщается и х=const. В этой области значений I1 статические механические характеристики двигателя описываются уравнением (3.101) при р=0:

где

На рис.3.42,а представлено семейство характеристик w=f(М), соответствующих ряду значений частоты f1 при Im£Imнас. Так как зависимость M=f(sa) (3.109) инвариантна относительно частоты, то при изменении f1 изменяется только скорость идеального холостого хода w0=2pf1/pп, а форма механических характеристик относительно этой точки не претерпевает изменений. Особенностью этих характеристик является малость критического скольжения sK1, по сравнению с sk, соответствующим питанию от источника напряжения, обусловленная тем, что хmн>>х1н+х'2н.
Однако при I1£Imнас невелико и значение Мк1. Поэтому для получения требуемой перегрузочной способности, аналогичной перегрузочной способности на естественной характеристике, в режиме питания от источника тока необходимо выбирать значения

При I1>>Imнас и идеальном холостом ходе магнитная цепь машины находится в глубоком насыщении, поэтому при малых значениях sa можно без большой погрешности принять Ф =Фmнас=const. С ростом скольжения намагничивающий ток Im уменьшается, однако в соответствии с принятой аппроксимацией до значения sa=sa.rp, при котором Im=Imнас, насыщение сохраняется. В области больших скольжений (sa> sa.rp), как показано на рис.3,41,a ток Im<Imнас, хm возрастает и приближенно может быть принято равным хmн (рис.3.41,б).
Отсюда следует, что при I1>>Imнас в области sa<sa.rp реальная форма кривой w=f(М) в значительной мере отклоняется от определяемой (3.109), а при больших скольжениях (sa> sarp) магнитная цепь размагничивается током ротора и реальная механическая характеристика сближается с рассчитываемой по (3.109). Принятая аппроксимация кривой намагничивания позволяет приближенно оценить вид механической характеристики при насыщении, которое соответствует области малых скольжений, т. е. рабочему ее участку. При насыщении Фm=Фmнас=const и ЭДС Е'2 при w0ном достигает значений, близких к U1ном. С учетом этого для режима насыщения можно принять E'2=U1ном=const и представить (3.109) в виде

где

Следовательно, насыщение смещает максимум момента в область больших скольжений, так как sk1нac>sk1.
Проведенный анализ влияния насыщения позволяет представить реальную форму механических характеристик при различных значениях I1. На рис.3.42,б приведены механические характеристики 1-3, соответствующие токам I11=Imнас, I12>Imнас И I13>I12, которые построены по (3.109) без учета насыщения. Там же показана механическая характеристика 4 для насыщенного состояния магнитной цепи, определяемая (3.110). Реальные механические характеристики (кривые 5-7) в области насыщения (sa<sа.гр) совпадают с кривой 4, а при отсутствии насыщения (sa>sа.гр) приближаются к соответствующим кривым 1-3.
Граничное скольжение sа.гр при I1=I11 равно нулю и с возрастанием тока I1 увеличивается. Соответственно при I11=Imнас магнитная цепь машины не насыщается при любых скольжениях и кривая 1 сливается с соответствующей реальной характеристикой 5. С увеличением I1 и возрастанием sагр увеличивается зона, где механические характеристики совпадают с кривой 4, а зона, в которой они совпадают с рассчитываемыми без учета насыщения, постепенно сокращается. Это, как видно на рис.3.42,б, приводит к постепенному увеличению критического скольжения.
Сравнивая уравнение механической характеристики для динамических процессов (3.101) с уравнением (3.92), соответствующим питанию двигателя от источника напряжения, можно установить, что они совпадают по форме и отличаются лишь выражениями критического момента и электромагнитной постоянной времени.
Следовательно, выполнив линеаризацию уравнения (3.101) в окрестности точки М°=0, s°а= 0 аналогично линеаризации, выполненной для уравнения (3.92), получим приближенное линеаризованное уравнение механической характеристики в виде

где b1=2Мк1/w0ном·sk1.
Передаточная функция динамической жесткости

Структурная схема электромеханического преобразования энергии при питании от источника тока в соответствии с (3.111) совпадает с полученной выше схемой для питания от источника напряжения и приведенной на рис.3.38. Однако динамические свойства в этих режимах существенно различны в связи с тем, что при питании от источника тока поток при I1=const изменяется в широких пределах. Изменения главного потока машины при этом определяют существенно большую инерционность электромеханического преобразователя, чем при питании от источника напряжения. Действительно, сравнивая

можно убедиться, что Тэ<<Тэ1 С ростом тока статора вследствие насыщения индуктивное сопротивление намагничивания х уменьшается, при этом уменьшается и электромагнитная постоянная Tэ1, стремясь при больших насыщениях к Тэ.
В отличие от питания от источника напряжения при питании от источника тока можно изменять частоту, не изменяя сигнала задания тока. Однако практически и в этом случае для обеспечения определенных условий протекания процессов электромеханического преобразования энергии задание тока в схеме рис.3.39 изменяют в функции задания частоты по тем или иным законам частотного управления.