Особенности частотного регулирования скорости асинхронного электропривода

При рассмотрении вопросов частотного регулирования момента уже было отмечено, что по сравнению с системой постоянного тока, управляемой путем изменения напряжения в цепи якоря, частотное регулирование реализуется более сложно в связи с отсутствием отдельного независимого канала регулирования потока двигателя, каким является обмотка возбуждения двигателя постоянного тока. Другой особенностью является сложность измерения ряда координат асинхронного электропривода, обусловленная работой двигателя на переменном токе.

Как следствие, в замкнутых системах частотного регулирования скорости для регулирования потока и момента двигателя широко используются положительные обратные связи, компенсирующие те или иные возмущения, а также косвенные методы измерения переменных.

В тех случаях, когда высоких требований к переходным процессам пуска, реверса и торможения не предъявляется и главным является обеспечение высокой точности регулирования скорости, в системе частотного регулирования обычно предусматривается канал регулирования магнитного потока по отклонению, реализуемый в двух вариантах. В первом исполнении применяют датчики Холла, сигналы которых примерно пропорциональны магнитному потоку в воздушном зазоре двигателя, т.е. используют прямое измерение магнитного потока для осуществления отрицательной связи, поддерживающей поток на заданном уровне. Во втором исполнении прибегают к косвенному измерению магнитного потока, в основе которого лежит векторное уравнение электрического равновесия для цепи статора в осях х,у:

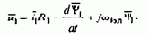
Выразив в нем потокосцепление через токи с помощью уравнения

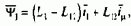
получим

Нетрудно видеть, что уравнение (8.96) устанавливает определенную зависимость намагничивающего тока Im а следовательно, и результирующего магнитного потока Ф от напряжения и тока статора при данных параметрах машины. Эта зависимость является векторной и в динамике осложняется наличием производных

. Тем не менее, полагая в режимах стабилизации потока im=const, d

/dt=0, с помощью современных вычислительных устройств можно по измеренным реальным напряжениям и токам двух фаз статора и известной частоте w0эл определять значения амплитуды и фазы магнитного потока и, таким образом, косвенным путем формировать сигнал отрицательной связи по мгновенным значениям потока, воздействующей на цепь задания напряжения или тока статора.

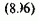
В тех случаях, когда частотное управление должно обеспечивать не только регулирование скорости, но и формирование равномерно ускоренного характера протекания всех переходных процессов, ограничение момента при механических перегрузках и т п., система регулирования скорости должна содержать подчиненный контур регулирования момента. В простейшем случае можно использовать уже рассмотренную компенсационную систему регулирования момента (см. рис.7.20).

Схема регулирования скорости асинхронного двигателя при этом дополняется регулятором скорости PC и отрицательной обратной связью по скорости, как показано на рис.8.36,a. Структурная схема представлена на рис.8.36,б, в ней контур регулирования момента представлен передаточной функцией, соответствующей (7.66), а в передаточной функции пропорционального PC учтена малая постоянная времени Тф фильтра в цепи обратной связи по скорости. С помощью этой схемы можно записать:

Уравнение динамической механической характеристики замкнутой по скорости системы электропривода

где w0зс=U3С/k0с - скорость идеального холостого хода.

Передаточная функция динамической жесткости механической характеристики

где Тm=Тэ+Tф - суммарная малая постоянная контура регулирования скорости.

Уравнение статической механической характеристики

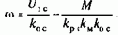
Модуль статической жесткости

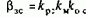
пропорционален коэффициенту обратной связи по скорости и теоретически может быть получен любого требуемого значения. Однако практически без динамической коррекции возможная жесткость механической характеристики в замкнутой системе, как было установлено в §8.5, ограничивается ростом колебательности электропривода с ростом kос.

Передаточная функция разомкнутого контура регулирования в соответствии с рис.8.36,б имеет вид

Отнесем постоянные Tф и Тэ к малым некомпенсируемым постоянным и в качестве оценки их влияния примем Tm=Tф+Тэ. Тогда (8.98) можно представить в виде

где T0=bTM/kockPCkM.

Сравнив (8.99) с (6.31), можно убедиться, что при этих условиях передаточная функция рассматриваемого разомкнутого контура совпадает по форме с желаемой передаточной функцией при настройке контура на технический оптимум.

Для получения такой настройки нужно выбрать koс из условия То=2Тm.

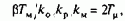
откуда

Значения kос, соответствующие выражению (8.100), для приводов малой и средней мощности при малой постоянной времени ТM получаются небольшими, и жесткость механических характеристик в замкнутой системе невысока. При показанной на рис.8.36,в форме характеристики регулятора скорости механические характеристики подобны характеристикам электропривода постоянного тока с двухконтурной системой подчиненного регулирования тока и скорости двигателя (рис.8.36,в).

Более высокую точность регулирования скорости могут обеспечить использование ПИ-регулятора скорости и выбор параметров по настройке на симметричный оптимум.

Компенсационный принцип стабилизации магнитного потока, использованный в данной схеме, не может обеспечить высокой точности регулирования, так как параметры двигателя при работе претерпевают изменения, вызванные изменениями температуры обмоток, не остается постоянным напряжение сети и т. п. Поэтому при высоких требованиях к точности необходимо сочетание регулирования по отклонению с компенсацией возмущений.

Содержание раздела