Динамика электропривода с синхронным двигателем
Анализируя структурную схему на рис.4.4, можно установить, что при работе в синхронном режиме переходные процессы синхронного электропривода могут быть вызваны изменениями управляющих воздействий и возмущениями в механической части. Управляющими воздействиями являются напряжения на обмотках статора u1 частота f1 и пропорциональная ей угловая скорость поля w0, напряжение uв, приложенное к обмотке возбуждения. Возмущающими воздействиями в механической части являются моменты нагрузки Мс1 и Мс2, изменения которых вызываются технологическими причинами.
При питании двигателя от сети его пуск осуществляется в асинхронном режиме с помощью предусмотренной для этой цели на роторе короткозамкнутой пусковой (демпферной) обмотки. В этом режиме электропривод ускоряется до подсинхронной скорости wвх, при которой обмотка возбуждения включается на постоянное напряжение UB и происходит процесс втягивания двигателя в синхронизм. Переходные процессы, протекающие при вхождении двигателя в синхронизм, имеют важное практическое значение, и их особенности необходимо в дальнейшем проанализировать.
Напряжение U1max частота f1 при питании от сети могут изменяться лишь в связи с колебаниями напряжения и частоты сети, обусловленными изменениями ее нагрузки. Эти колебания ограничены действующими нормами, поэтому невелики и здесь могут не учитываться.
Анализ переходных процессов, возникающих при изменениях напряжения возбуждения обмотки ротора UB, представляет интерес в тех случаях, когда предусматривается автоматическое регулирование тока возбуждения для регулирования cos ф двигателя.
Основными возмущениями при питании от сети следует считать возможные изменения нагрузки электропривода. При ударном характере нагрузки, в процессах приложения и снятия нагрузки и, как было отмечено, в процессах втягивания в синхронизм динамические свойства синхронного электропривода проявляются достаточно полно, и на их рассмотрении здесь необходимо сосредоточить основное внимание.
В §3.15 было отмечено, что электромагнитная связь возбужденного ротора с полем статора аналогична упругой механической связи.
Влияние этой связи на динамику синхронного электропривода можно проанализировать при представлении механической части жестким приведенным звеном с помощью структурной схемы на рис.4.6, полученной при с12=¥ и линеаризации угловой характеристики двигателя. Эта схема при отсутствии у двигателя демпферной обмотки (b=0) показана на рис.4.37. Из рисунка видно, что при жестких механических связях синхронный электропривод без демпферной обмотки неработоспособен. Действительно, два интегрирующих звена, охваченных жесткой отрицательной обратной связью, как известно из теории автоматического управления, образуют недемпфированную колебательную систему с передаточной функцией

и частотой свободных колебаний
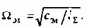
Демпферная обмотка создает асинхронный момент, который обеспечивает затухание колебаний в системе. В соответствии с рис.4.6 при этом

где Tм=JS/b - электромеханическая постоянная времени.

Передаточная функция электропривода по возмущению Мс может быть также определена по структурной схеме рис.4.6 и представлена в виде

В ряде случаев представляет интерес передаточная функция синхронного электропривода, в которой выходной переменной является угол q=f0-f, или, что то же, синхронная составляющая момента двигателя Mсин»сэмq. Эту передаточную функцию получаем из (4.109), учитывая, что при w0=0, w=-Dw и q есть интеграл от Dw по времени:
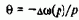
Следовательно, функция (4.109) может быть представлена в виде

Соответствующая АФХ

Амплитудно-частотная характеристика

Фазо-частотная характеристика

Если известно, что момент нагрузки электропривода изменяется по закону Мс=Мс.max·sinWt, с помощью (4.112) и (4.113) можно определить зависимость угла 0 от времени в виде
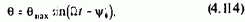
где

Рассматривая полученные зависимости, можно установить, что они соответствуют колебательному звену с коэффициентом затухания, определяемым электромеханической постоянной Тм. Следовательно, при данном JS колебательность определяется модулем жесткости асинхронной механической характеристики b. Чем больше модуль жесткости, тем меньше при колебаниях нагрузки Мc амплитуда колебаний синхронной составляющей момента, тем меньше резонансное усиление колебаний при частоте, близкой частоте свободных колебаний Wэм.
Если сравнить передаточную функцию (4.31) упругой электромеханической системы, соответствующую J2=¥, g=¥ и Тэ=0, с передаточной функцией синхронного электропривода (4.110), можно убедиться, что их характеристические уравнения полностью совпадают. Это означает, что электропривод с синхронным двигателем эквивалентен асинхронному электроприводу с упругой механической связью при бесконечно большой массе механизма Роль упругой механической связи при этом выполняют силы электромагнитного взаимодействия между полями ротора и статора.
Структурная схема рис.4.6 и соответствующие ей передаточные функции синхронного электропривода при принятых допущениях могут быть использованы для анализа переходных процессов при приложении и снятии нагрузки. Дифференциальное уравнение системы относительно скорости двигателя w можно записать с помощью (4.108):

При питании от сети w0=const, dw0/dt=0 Уравнение, (4.115) при этом имеет вид

Корни характеристического уравнения

Если Wэм>1/2TM, корни являются комплексно-сопряженными:
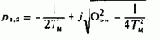
Следовательно, решение (4.115) необходимо искать в виде

Значения А и В могут быть определены с помощью начальных условий: при t=0 (w)0=wнaч, (dw/dt)0=(Мнач-МС)/JS, причем


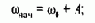
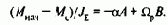
Откуда

Подставив А и В в (4.118), получим решение уравнения (4.116) в виде

Для получения уравнения системы относительно момента двигателя М определим по структурной схеме рис.4.6 передаточную функцию:

Откуда

При изменениях момента скачком при t>0, Мс=const. Соответственно для рассматриваемых процессов уравнение имеет вид

Решение (4.121) будем искать в виде

Значения С и D определяются по начальным условиям аналогично выполненному ранее расчету. С помощью уравнения механической характеристики найдем производную момента:

При t=0, М0=Мнач, а производная момента (dM/dt)0 вычисляется с помощью (4.122):


Определив с помощью начальных условий С и D получим решение M(t) в виде


Полученные решения (4 120) и (4.124) свидетельствуют о том, что при изменениях нагрузки скачком скорость синхронного электропривода совершает затухающие колебания относительно скорости поля, а его момент колеблется относительно момента Мс, постепенно затухая с коэффициентом затухания а.
Максимум момента и динамическое падение скорости при этом возрастают при увеличении скачка нагрузки и при увеличении начального отклонения скорости w от w0. Эти же показатели при прочих равных условиях уменьшаются при увеличении коэффициента затухания a.

Уравнение (4.124) получено при линеаризации угловой характеристики двигателя, поэтому оно даст удовлетворительные оценки показателей переходного процесса только при М£М=lМном.
Наличие демпферной обмотки позволяет осуществлять пуск синхронного двигателя путем прямого включения его на напряжение сети. Пусковые характеристики показаны на рис.4.38. Характеристика 1 соответствует относительно небольшому сопротивлению демпферной обмотки, при этом критическое скольжение мало, что увеличивает жесткость рабочего участка механической характеристики и уменьшает пусковой момент Мп. Характеристика 2 соответствует повышенному сопротивлению этой обмотки, поэтому имеет сниженную жесткость рабочего участка, но больший пусковой момент Мп.
С точки зрения условий асинхронного пуска двигателя до подсинхронной скорости wвх, которой соответствует скольжение sвх, предпочтительна характеристика 2, особенно при значительной нагрузке на валу.
При достижении двигателем подсинхронной скорости wвх в цепь обмотки возбуждения подается постоянный ток, магнитный поток возрастает до номинального значения и наступает второй этап пуска - втягивание двигателя в синхронизм. Строгий анализ этого режима осложняется протекающими электромагнитными процессами. В первом приближении для оценки условий втягивания в синхронизм можно воспользоваться (4.120) и (4.124).
Для удобства анализа этого процесса решение системы уравнений синхронного электропривода при допущениях, соответствующих (4.110), получают относительно угла q, изменения которого при втягивании в синхронизм заслуживают особого внимания. В отклонениях от точки статического равновесия это решение имеет следующий вид:


При одной и той же нагрузке статическая характеристика 2 на рис.4.38 обеспечивает меньшую начальную скорость при втягивании в синхронизм. Соответственно при этом sвх2>sвх1 и амплитуда колебаний угла Dqmax в (4.125) получается большей. Реальной угловой характеристике синхронного двигателя при больших Dq соответствуют уменьшающиеся значения сэм. Как следствие, с ростом sbx условия втягивания в синхронизм ухудшаются и при больших sвx синхронизация может оказаться невозможной.
Таким образом, более благоприятные условия втягивания в синхронизм обеспечиваются жесткой механической характеристикой 1. Практически пусковая обмотка рассчитывается так, чтобы обеспечивались удовлетворительные условия пуска при заданном максимальном значении нагрузки Мс mах, а значения входного скольжения лежали в допустимых пределах: sbx=0,03¸0,05.