Динамические свойства электропривода
При изучении свойств механической части электропривода было установлено, что во многих практических случаях влияние упругих колебаний на движение первой массы пренебрежимо мало. Имея в виду сочетания параметров механической части, при которых это условие выполняется, принимаем в (4.5) с12=¥, ф1=f2=ф, w1=w2=w. В результате получаем


Таким образом, рассмотрение свойств электромеханической системы, описываемой (4.11), дает представления о динамических особенностях большинства промышленных разомкнутых систем электропривода, при этом отдельного рассмотрения требуют лишь свойства синхронного электропривода в связи с отличием (4.10) от (4.11).
Для анализа свойств электропривода с линейной механической характеристикой как объекта автоматического управления получим передаточную функцию системы по управляющему воздействию. В соответствии с рис.4.7

где Тм=JS/b - электромеханическая постоянная времени. Передаточная функция по возмущающему воздействию - моменту статической нагрузки Мс - имеет вид

Характеристическое уравнение системы
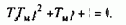
Корни характеристического уравнения

где m=ТM/ТЭ - отношение постоянных времени электропривода.
Значение m является важным показателем динамических свойств электропривода, непосредственно определяющим колебательность разомкнутой электромеханической системы при жестких механических связях. Если m>4, то
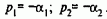
Соответственно передаточная функция (4.12) может быть при таких параметрах преобразована к виду

где T1=1/a1; Т2=1/a2.
Следовательно, при m>4 рассматриваемый электропривод для анализа может быть представлен в виде последовательного соединения двух инерционных звеньев с постоянными времени T1 и Т2 Частотные характеристики электропривода при таком сочетании параметров имеют вид, показанный на рис.4.8,a. Реакцию электропривода на скачок управляющего воздействия при нулевых начальных условиях и Мс=0 характеризуют соответствующие (4.15) переходная функция

и импульсная (весовая) функция


При m=4 характеристическое уравнение системы имеет два равных отрицательных корня: р12=-a=-1/2Тэ. В этом случае передаточная функция (4.12) преобразуется к виду

где T=1/а.

Графики переходной h(t) и весовой h'(t) функций построены на рис.4.9,б по выражениям
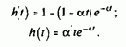
При сочетаниях параметров, которым соответствуют значения m<4, характеристическое уравнение имеет комплексно-сопряженные корни
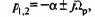
и электропривод представляет собой колебательное звено с коэффициентом затухания x<1, уменьшающимся по мере уменьшения т. Учитывая обозначения коэффициентов передаточной функции колебательного звена, принятые в теории управления, можно записать

С помощью (4.19) установим связь между параметрами электропривода и обобщенного колебательного звена:

Значениям m<4 соответствуют коэффициенты затухания x<1.

Частотные характеристики колебательного звена при m=0,5;2;4 (x=0,35;0,71;1) представлены на рис.4.10,а,б. Они показывают, что при уменьшении m колебательность электропривода возрастает и при m<2 (x<0,71) в ЛАЧХ проявляется резонансный пик, быстро возрастающий с уменьшением m. Переходная функция электропривода при m<4 выражается соотношением

Импульсная функция:

На рис.4.10,б представлен ряд зависимостей h(t*), где t*=t/Tэ, соответствующих тем же значениям m, что и на рис.4.10,а. Рассматривая (4.14) и (4.21), можно установить, что общее время затухания колебаний зависит только от Тэ Так как Тэ=TM/m при данной постоянной Tм, затухание и частота колебаний определяются соотношением постоянных m. Только от m зависит и показатель колебательности - логарифмический декремент колебаний:

При m=2 и l=6,28 колебания затухают практически за один период, а скорость электропривода достигает установившегося значения с небольшим превышением его в переходном процессе, составляющим около 5% установившегося значения. При m<2 затухание колебаний ухудшается, и в переходном процессе максимальные значения скорости все в большей мере превышают установившееся значение. При данном m общее время переходного процесса увеличивается пропорционально увеличению ТM. Представленные на рис.4.8-4.10 ЛФЧХ Y(W) свидетельствуют о том, что при одинаковом максимальном угле сдвига колебаний по фазе Ymax=-p с уменьшением m изменения фазы в области частоты недемпфированного электромеханического резонанса Wэм=1/T1=1/ÖТэТм становятся все более быстрыми.
Сравнивая (4.12) и (4.13), можно убедиться, что при колебаниях нагрузки электромагнитная инерция определяет при прочих равных условиях более высокие амплитуды колебаний скорости в области резонанса в связи с наличием в числителе (4.13) передаточной функции форсирующего звена с постоянной времени Тэ.
Таким образом, электропривод с линейной механической характеристикой вследствие электромагнитной инерции представляет собой при жестких механических связях колебательное звено, показатели колебательности которого l и x зависят только от соотношения постоянных времени m=ТМ/ТЭ, а быстродействие определяется электромагнитной постоянной времени Тэ или при данном m - электромеханической постоянной времени ТM.
При работе на естественной характеристике значения Тэ лежат в пределах Тэ=0,01¸0,1с, причем для асинхронных двигателей Тэ при питании от источника напряжения меньше, чем для двигателей постоянного тока той же мощности. Электромеханическая постоянная Тм изменяется в более широких пределах, и ее удобно выразить через расчетную величину - электромеханическую постоянную времени собственно двигателя - и отношение моментов инерции электропривода JS и якоря двигателя Jдв:

Для двигателей мощностью выше 10 кВт ориентировочно Т=0,01¸0,1 с, причем обычно постоянная времени TМ.ДВ соизмерима или близка Тэ. Поэтому для электроприводов с небольшим моментом инерции механизма наиболее вероятные значения m заключены в пределах 0,5<m<2, а для электроприводов со значительной инерцией механизма m>2. Из изложенного следует, что в этих пределах резонансное усиление колебаний невелико и электропривод представляет собой колебательное звено с высоким коэффициентом демпфирования x>0,4.
Это обстоятельство при рассмотрении электропривода с линейной механической характеристикой как объекта автоматического регулирования позволяет прибегать к упрощенному представлению передаточной функции (4.12) в виде

т. е. заменять колебательное звено двумя апериодическими с постоянной Т1=ÖTэTM.
Асимптотическая ЛАЧХ, соответствующая (4.24), при W<1/ Т1 имеет вид горизонтальной прямой, совпадающей с осью абсцисс, а при W>l/T1, представляет собой прямую с наклоном -40 дБ/дек (штриховая линия на рис.4.10,а). Сравнивая эту зависимость с реальными ЛАЧХ колебательного звена при различных значениях x, можно установить, что при x>0,4 расхождения незначительны. Погрешность в сторону занижения амплитуды при x>0,4 не превышает 3 дБ, что обычно допустимо.
Для многих электроприводов малой мощности m>4, при этом можно пренебречь электромагнитной инерцией, положив в (4.11)



построены на рис.4.11,г. С помощью этого рисунка можно пояснить физический смысл электромеханической постоянной времени. Электромеханическая постоянная Тм представляет собой время, за которое электропривод достиг бы установившейся скорости, двигаясь равномерно ускоренно под действием постоянного динамического момента, равного начальному значению:
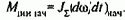
Сравнивая кривые, приведенные на рис.4.11, с аналогичными кривыми на рис.4.8, которые соответствуют m>4 при учете электромагнитной инерции, можно сделать следующие выводы. При анализе переходных процессов в разомкнутой системе электропривода при m>4, как правило, можно без большой погрешности пренебрегать влиянием электромагнитной инерции и принимать Тэ»0. При синтезе замкнутых систем регулирования координат электромеханической системы малую постоянную Тэ при m>4 следует учитывать во избежание ошибок, вносимых неучетом потери запаса по фазе на частоте среза контура регулирования, обусловленной электромагнитной инерцией электромеханического преобразователя.
