Динамические свойства электромеханического преобразователя с независимым возбуждением
Рассмотренные выше характеристики двигателя с независимым возбуждением получены в предположении, что двигатель питается от бесконечно мощной сети или от любого другого источника, обладающего свойствами источника напряжения с внутренним сопротивлением, равным нулю. Приступая к изучению динамических свойств, необходимо иметь в виду, что в регулируемом электроприводе возможно питание якорной цепи двигателя и от преобразователей, обладающих свойствами источника тока. Поэтому анализ динамических свойств электромеханического преобразрвателя с независимым возбуждением проведем для случаев питания как от источника напряжения, так и от источника тока.
Для анализа воспользуемся системой (3.6). Обозначив d/dt=р, запишем ее в виде

где Tв=Lв/Rв - электромагнитная постоянная времени обмотки возбуждения; Тя=LяS/Rя - электромагнитная постоянная времени цепи якоря; kф=Ф/iв - коэффициент, соответствующий линейной части кривой намагничивания двигателя.
Структурная схема электромеханического преобразования энергии, соответствующая (3.40), приведена на рис.3.11,а. На схеме представлены два возможных канала управления при питании от источника напряжения - канал управления полем двигателя, которому соответствует управляющее воздействие uв, и канал управления по цепи якоря с управляющим воздействием ия. Из схемы следует, что при отсутствии реакции якоря процессы в цепи возбуждения протекают независимо от процессов в якорной цепи, а процессы в якорной цепи зависят от изменений магнитного потока двигателя Ф.

Цепь возбуждения двигателя представляет собой апериодическое звено с постоянной времени Тъ, Индуктивность LB обмотки возбуждения может быть определена по формуле
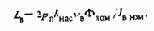
где kнас=Iвном/Iвлин - коэффициент насыщения; Iвлин - ток возбуждения, создающий номинальный поток Фном при отсутствии насыщения магнитной цепи.
Значение индуктивности LB, определяемое данной формулой, соответствует линейной части кривой намагничивания. При работе в насыщенной части кривой намагничивания индуктивность и постоянная времени цепи возбуждения уменьшаются тем больше, чем выше насыщение:
Полученное в §3.6 математическое описание процессов электромеханического преобразования энергии в двигателе с последовательным возбуждением содержит произведения переменных, поэтому использовать его для анализа динамических свойств преобразователя можно лишь с помощью ЭВМ. Однако общие закономерности, основные динамические свойства электромеханического преобразователя с последовательным возбуждением могут быть выявлены аналитическим путем, если осуществить линеаризацию уравнений механической характеристики (3.50) в окрестности точки статического равновесия.



Tв- постоянные времени соответственно эквивалентного контура вихревых токов (см. рис.3.15,б) и обмотки возбуждения. Вычтя почленно из первого уравнения второе, получим более удобный для решения вид системы (3.50):

Линеаризуем систему (3.57) путем разложения в ряд Тэйлора в окрестности точки статического равновесия, обозначим d/dt=р, получим

Решив систему (3.58) относительно Д/я и DМ, получим линеаризованные уравнения электромеханической и механической характеристик двигателя в виде

Уравнения (3.59) и (3.60) характеризуют основные динамические особенности преобразователя с последовательным возбуждением при условии ограничения отклонения переменных от точки статического равновесия узкими пределами. Сравнивая их, можно установить, что наличие контура вихревых токов определяет более значительные колебания тока, чем момента при тех же условиях. Это различие существенно усиливается, если не учитывать индуктивности рассеяния якорной цепи, положив Тя=0. При этом порядок числителя и порядок знаменателя (3.59) становятся одинаковыми, что свидетельствует о возможности изменения тока якоря скачком и существенно искажает действительный характер процессов.
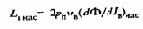
При отсутствии добавочных резисторов у двигателей мощностью от 1 до нескольких тысяч киловатт постоянная времени цепи возбуждения лежит в пределах Tв=0,2¸5 с, причем с увеличением мощности двигателя она быстро возрастает.
Изменение потока вносит нелинейность в математическое описание процессов преобразования энергии даже при ненасыщенной магнитной цепи, поэтому при переменном магнитном потоке структура на рис 3.11,a используется для анализа динамических свойств электропривода постоянного тока с помощью ЭВМ. Для синтеза регулируемых электроприводов математическое описание электромеханического преобразователя линеаризуется путем разложения в ряд Тэйлора в окрестности точки статического равновесия.
При питании от источника напряжения двигатель с независимым возбуждением работает преимущественно при постоянном потоке: Ф=Фном=const, при этом уравнение механической характеристики двигателя в соответствии с (3.7) принимает вид

Этому уравнению соответствует структурная схема преобразователя, представленная на рис.3.11,б. Она свидетельствует о том, что при Ф=const электромеханический преобразователь представляет собой апериодическое звено с постоянной времени Тя. Индуктивность рассеяния якорной цепи двигателя может быть вычислена по приближенной формуле

где g=0,6 для некомпенсированных и g=0,25 для компенсированных двигателей.
Постоянная времени якорной цепи двигателей средней и большой мощности лежит в пределах Тя=0,02¸0,1 с, причем наибольшие значения соответствуют некомпенсированным либо тихоходным двигателям большой мощности.
Уравнение динамической механической характеристики устанавливает связь между механическими переменными в общем виде, справедливом для любых режимов работы электропривода. Форма конкретных динамических характеристик определяется совокупностью условий и связей, наложенных на движение электромеханической системы в данном процессе. Поэтому двигатель имеет бесчисленное множество динамических характеристик, соответствующих переходным процессам и зависящих от вида механической части, начальных условий, уровня и характера управляющих и возмущающих воздействий.
Эти характеристики несут информацию о свойствах динамической системы, состоящей из электромеханического преобразователя энергии и механической части, а для анализа электромеханических свойств самого преобразователя их непосредственно использовать нельзя.

 |
Тогда (3.41) при p=d/dt однозначно определяет соответствующий закон изменения скорости:

На рис.3.12 показаны характеристики w(t) и M(t) и соответствующая им динамическая характеристика - замкнутая кривая 1. Нетрудно видеть, что электромагнитная инерция якорной цепи вызывает значительные отклонения динамической характеристики 1 от статической 2. Уменьшение частоты вынужденных колебаний W. или соответствующее снижение постоянной времени Тя приводят к уменьшению этих отклонений (кривая 3), и в пределе при Тя®0 или Q®0 динамическая характеристика сливается со статической.
Эти рассуждения приводят к выводу о целесообразности использования для анализа динамических свойств двигателя частотного метода. Для этой цели с помощью структурной схемы рис.3.11,б определим передаточную функцию динамической жесткости механической характеристики (см. гл. 2)


Амплитудно-фазовую характеристику динамической жесткости получим подстановкой в (3.44) p=jW.:

Соответствующие (3.45) АЧХ и ФЧХ динамической жесткости

Амплитудно-фазовая характеристика динамической жесткости (3.45) представлена на рис.3.13,а, а на рис.3.13,б показаны соответствующие ей ЛАЧХ и Л ФЧХ. Рассматривая их, можно установить, что электромагнитная инерция приводит к уменьшению модуля динамической жесткости тем в большей степени, чем выше частота вынужденных колебаний Л.
Одновременно сдвиг по фазе между колебаниями скорости и момента изменяется от -180°, соответствующих статической жесткости (W=0), до -270° при Q®¥. Введение добавочных резисторов в цепь якоря уменьшает Tя, при этом, если в пределах возможных частот колебаний модуль динамической жесткости снижается незначительно, а фазовый сдвиг остается близким к 180°, можно без существенных погрешностей исследовать динамические процессы, пользуясь выражением статической механической характеристики.
Частотные характеристики динамической жесткости упрощают определение зависимости от времени одной из механических переменных по известной для установившегося колебательного режима другой. Если, как было принято выше, М=Мср+DMmax·sinW·t, зависимость w(t) определится соотношением

Зависимость М(t) по заданной функции w(t)=Dwmax·sinW·t определяется аналогичным путем:

Таким образом, суждение о жесткости естественной механической характеристики по статической зависимости М=f(w) и по модулю статической жесткости b дает правильные представления лишь для статических режимов или при достаточно плавных изменениях нагрузки. При изменениях нагрузки скачком, а также в установившихся колебательных режимах динамическая характеристика может существенно отклоняться от статической, и необходимо оценивать эти отклонения с помощью частотных характеристик динамической жесткости либо путем расчета соответствующего переходного процесса с учетом электромагнитной инерции двигателя.
Достоинством электромеханического преобразователя с независимым возбуждением при Ф=const является высокое быстродействие, определяемое относительно небольшой постоянной времени Тя. При этом следует иметь в виду, что проведенный анализ динамических свойств преобразователя полностью справедлив только для компенсированных двигателей. У некомпенсированных двигателей, как было отмечено выше, вследствие реакции якоря магнитный поток при изменениях тока якоря не остается постоянным, а может изменяться на 10-20 % в сторону уменьшения от Ф0.
Изменения основного потока машины происходят с постоянной времени цепи возбуждения Tв, намного большей, чем Тя. Соответственно инерционность преобразователя при проявлениях реакции якоря возрастает и расхождения между статическими и динамическими характеристиками проявляются при меньших частотах.
При питании якоря двигателя от источника тока iя=Iя1=const при любых изменениях ЭДС двигателя. Система (3.40) при этом приводится к следующему уравнению механической характеристики:

Рис 3.14 Статическая 1 и динамическая 2 характеристики двигателя П62
Этому уравнению соответствует структура электромеханического преобразователя, представленная на рис.3 11,в. Сравнивая рис.3.11,б и в, можно установить, что в режиме питания якоря от источника тока двигатель с независимым возбуждением утрачивает рассмотренные выше электромеханические свойства. Отсутствие зависимости тока якоря от скорости исключает проявление электромеханической связи, и статическая механическая характеристика двигателя М=f(w) при ub=const обладает жесткостью, равной нулю.
Как объект управления электромеханический преобразователь при этом представляет собой апериодическое звено с большой постоянной времени Tв, управляющим воздействием является напряжение, приложенное к обмотке возбуждения uя. В соответствии с рис.3.11,в электромеханический преобразователь при Iя=const является источником момента М=const, значения которого можно регулировать путем воздействия на инерционный канал возбуждения двигателя.
Поэтому во всех случаях, когда ставится задача оценки характера изменения тока и его значения в том или ином динамическом режиме, следует пользоваться уравнением (3.59), не прибегая к дополнительным упрощениям.

Структурная схема линеаризованного электромеханического преобразователя с последовательным возбуждением, соответствующая (3.60), представлена на рис.3.23. С помощью этой схемы определим передаточную функцию динамической жесткости механической характеристики:

Уравнение (3.61) свидетельствует о том, что динамическая жесткость в данном случае существенно зависит от положения точки статического равновесия на механической характеристике двигателя. При этом следует иметь в виду, что каждой точке статической характеристики соответствуют не только различные значения Ф°, Iя°, w0, но также и различные значения таких параметров, как TвS и k'ф. При уменьшении момента двигателя по сравнению с номинальным (М°<Мном) коэффициент k'ф возрастает и при уменьшении потока до значений, соответствующих линейной части кривой намагничивания, становится равным коэффициенту k'фmах=k'ф [см. рис.3.16 и формулы (3.53) и (3.54)]. При дальнейшем уменьшении момента и потока kф остается постоянным, соответственно максимально и постоянно значение TвS. В области перегрузок (М°>Мном) магнитная цепь двигателя насыщается, соответственно k'ф и TвS принимают достаточно малые значения.
Если учесть, что Тя и TВТ при I°я<Iном намного меньше, чем TBS и их произведение в (3.61) можно приближенно принять равным нулю, то для приближенных оценок получаем удобную формулу:

где


Формула (3.62) аналогична по форме формуле динамической жесткости двигателя с независимым возбуждением (3.44), но по существу отличается непостоянством модуля и эквивалентной электромагнитной постоянной в различных точках статической характеристики при I°я<Iном. Если магнитная цепь двигателя ненасыщенна, т. е. kф=k'ф=const, то k'фI°я=Ф°, и модуль статической жесткости определяется соотношением
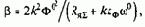
из которого следует, что с уменьшением нагрузки статическая жесткость механической характеристики уменьшается весьма быстро как из-за уменьшения потока Ф°, так и из-за возрастания скорости w°. Модуль динамической жесткости при этом дополнительно снижается за счет электромагнитной инерции, характеризуемой постоянной времени Тэ так же, как и у двигателя с независимым возбуждением. При сопоставлении необходимо иметь в виду, что сумма TвS+Тя при ненасыщенной машине намного превосходит значение Тя для двигателя с независимым возбуждением, но включение обмотки возбуждения в силовую цепь приводит к тому, что Tэ зависит от скорости w0 и существенно снижается при увеличении скорости. В области насыщения при I°я>Iном k'ф»0 и ТВS - стремится к значению, соответствующему индуктивности рассеяния обмотки возбуждения, при этом b=k2Ф2/RЯS и Тэ=Тя=LЯS, где LяS - суммарная индуктивность рассеяния якорной цепи. Таким образом, в области перегрузок динамические свойства двигателя с последовательным возбуждением практически совпадают с рассмотренными выше свойствами двигателя с независимым возбуждением.
Линеаризованные характеристики двигателя с последовательным возбуждением (3.59) и (3.60) могут быть использованы для анализа установившихся колебательных режимов электромеханических систем с двигателем последовательного возбуждения, а также для проверки устойчивости и качества замкнутых систем регулирования с таким двигателем при малых отклонениях от положения статического равновесия.
