Динамические свойства асинхронного
Математическое описание динамических процессов преобразования энергии в §3.10 было получено в предположении, что двигатель получает питание от сети или от индивидуального преобразователя, обладающего свойствами источника напряжения, т. е. источника, напряжение которого при изменении тока нагрузки остается неизменным. Проведем с его помощью анализ динамических свойств асинхронного преобразователя, рассматривая его как объект управления. Как было показано, для реализации управления моментом и скоростью двигателя в широких пределах при благоприятных условиях необходимо изменять частоту подведенного напряжения, воздействуя на скорость поля и амплитуду напряжения, определяющую при данной частоте магнитный поток двигателя.
Анализ динамических процессов преобразования энергии в асинхронном двигателе представляет собой сложную задачу в связи с существенной нелинейностью уравнений (3.64) и (3.68), обусловленной наличием произведений переменных. Исследование динамических процессов при широких пределах изменения скорости целесообразно вести с применением вычислительной техники. Для этих целей удобную форму математического описания дает (3.68), если решить каждое уравнение относительно производной потокосцепления и записать:




Здесь рассматривается динамический режим работы двигателя, имеющий место по истечении времени после подключения к источнику переменного напряжения, достаточного для затухания свободных составляющих, обусловленных переходным процессом включения. При этом предполагается, что отклонения скорости от значения, определяемого статической характеристикой, малы, а изменения токов не вызывают существенных изменений потокосцепления статора

Для этих условий, положив d

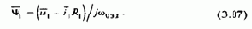
Следовательно, при питании от источника напряжения при неизменной частоте w0эл=const изменения Y1 вызываются только изменениями падения напряжения на активном сопротивлении статора R1 Если принять R1=0, то при неизменной частоте постоянство



Соотношение (3.88) определяет закон частотного управления U1/f1=const.
Пусть к обмоткам статора обобщенной машины приложена система синусоидальных напряжений, которым соответствует изображающий вектор

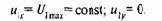
Тогда в соответствии с (3.88)
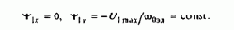
Таким образом, для рассматриваемых условий процессы электромеханического преобразования в асинхронном двигателе описываются тремя последними уравнениями системы (3.86). Выполним вспомогательные преобразования:

Здесь индексом «н» обозначено, что индуктивные сопротивления х1н, x2н, хmн соответствуют номинальной частоте сети w0элном; учтено, что хmн>>х,н; sk определено из (3.77) при R1=0. С учетом полученных значений Y1x и Y1у и последнего соотношения три указанных уравнения системы (3.86) запишутся в виде

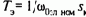
здесь
- электромагнитная постоянная времени;

абсолютное скольжение, равное отношению отклонения скорости двигателя w от скорости поля w0 при любой частоте f1 к скорости поля w0ном при частоте f1ном.
Положим d/dt=р и произведем преобразования алгебраизированных уравнений (3.89), имея в виду, что эти уравнения нелинейны и поэтому допустимы только такие их преобразования, при которых строго сохраняется предусмотренный исходными уравнениями порядок дифференцирования переменных.
С этой целью вначале из первого уравнения определим Y2:
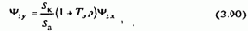
Подставив (3.90) во второе уравнение системы (3.89) с соблюдением получающегося порядка дифференцирования переменных, получим

Подстановка (3.91) в третье уравнение системы (3.89) дает искомое выражение механической характеристики:

где

В последней записи критического момента Мк произведен переход от максимального напряжения U1max двухфазной модели двигателя к реальному действующему значению напряжения на фазе трехфазного двигателя U1. По формуле (2.37)

Кроме того, учтено, что хmн>>х1н и хmн>>х'2н. Нетрудно убедиться, что полученное значение Mk совпадает с определяемым по (3.78) при R1=0 и w0=w0 ном. Таким образом, полученное приближенное уравнение механической характеристики в качестве частного случая статического режима работы (р=0) дает уравнение статической механической характеристики (3.79) при R1»0. Однако оно выражено в функции абсолютного скольжения Sa:

поэтому не только приближенно описывает естественную характеристику двигателя (w0=w0ном), но и определяет искусственные механические характеристики двигателя, соответствующие различной частоте питающего напряжения f1 при изменении напряжения по закону U1/f1=const. Как следует из (3.93) и выражения Мк в (3.92), при R1=0 механические характеристики инвариантны относительно абсолютного скольжения sa и представляются зависимостями w=f(М), показанными для различных частот пунктирными кривыми на рис.3.37. Реально в (3.87) можно пренебрегать R1 только при частотах, близких к номинальной, при этом U1=U1ном>>I1R1. При снижении частоты и напряжения по закону U1/f1=const, как показывает (3.87), потокосцепление Y1 должно снижаться, стремясь к 0 при f1®0. Соответственно с учетом R1¹0 реальные механические характеристики при таком законе управления имеют снижающийся при малых частотах критический момент (см. сплошные кривые на рис.3.37). По этой причине в реальных системах используются более сложные законы частотного управления, рассматриваемые в гл. 7.
Уравнение механической характеристики ( 3 92) отражает влияние электромагнитной инерции на протекание динамических процессов электромеханического преобразования энергии при ограниченных по амплитуде колебаниях в окрестностях точек статической характеристики. Для анализа этого влияния осуществим линеаризацию этого уравнения. Вначале необходимо выполнить операции дифференцирования в последовательности, полученной при выводе (3.92)
 |

После дифференцирования получим
 |
Раскладываем полученное уравнение в ряд Тэйлора в окрестности точки М°, s°a, пренебрегая членами высшего порядка малости. После преобразований уравнение механической характеристики представляется в виде

Уравнение (3.94) позволяет анализировать модуль статической жесткости линеаризованной механической характеристики и влияние электромагнитной инерции при линеаризации в любой точке статической механической характеристики M°=f(s°). Наибольший интерес представляет линеаризованное уравнение механической характеристики для рабочего участка sa<sk. Такое уравнение получим с помощью (3.94), положив s0a=0,Dsа=sa-s0a=sa=(w0-w)/w0ном;DM=M-M0=M

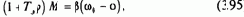 |
Следовательно, в окрестности точки М°=0, s0a=0 электромеханический преобразователь представляется звеном первого порядка, так как его уравнение механической характеристики имеет вид
где b=2·Мк/w0ном·sк - модуль жесткости линеаризованной механической характеристики.

Передаточная функция динамической жесткости в соответствии с этой схемой запишется так:

Сравнивая (3.95) и (3.96) с аналогичными формулами для двигателя постоянного тока с независимым возбуждением, можно заключить, что в пределах рабочего участка асинхронный двигатель имеет динамические свойства, аналогичные динамическим свойствам двигателя с независимым возбуждением.
Так как критическое скольжение двигателей лежит в пределах sk=0,05¸0,5, причем меньшие значения соответствуют мощным двигателям, электромагнитная постоянная двигателя Тэ при питании от источника напряжения невелика:

меньшие значения соответствуют двигателям малой мощности.