Деревья

Деревья являются одним из интереснейших классов графов, используемых для представления различного рода иерахических структур.

Определение 1.10. Граф

называется деревом, если

1. в нем есть одна вершина
   
   , в которую не входят ребра; она называется корнем дерева;
2. в каждую из остальных вершин входит ровно по одному ребру;
3. все вершины достижимы из корня.

На рисунке 2 показан пример дерева

С ориентированными деревьями связана богатая терминология, пришедшая из двух источников: ботаники и области семейных отношений.

Корень - это единственная вершина, в которую не входят ребра, листья - это вершины, из которых не выходят ребра. Путь из корня в лист называется ветвью дерева. Высота дерева - это максимальная из длин его ветвей. Глубина вершины - это длина пути из корня в эту вершину. Для вершины

, подграф дерева , включающий все достижимые из вершины и соединяющие их ребра из , образует поддерево дерева с корнем . Высота вершины - это высота дерева . Граф, являющийся объединением нескольких непересекающихся деревьев, называется лесом.

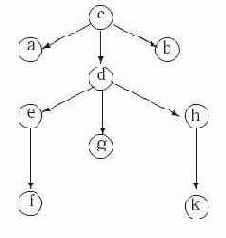
Рис. 1.2.  Дерево G1

Если из вершины

ведет ребро в вершину , то называется отцом , а - сыном (в последнее время в ангоязычной литературе употребляется асексульная пара терминов: родитель - ребенок). Из определения дерева непосредственно следует, что у каждой вершины кроме корня имеется единственный отец. Если из вершины ведет путь в вершину , то называется предком , а - потомком . Вершины, у которых общий отец, называются братьями

или сестрами.

Пример 1.4. В дереве на рис. 1.2

вершина

является корнем, вершины - листья. Путь - одна из ветвей дерева . Вершина является отцом (родителем) вершин и а каждая из этих вершин - ее сыном (ребенком). Между собой вершины и являются братьями (сестрами). Глубина равна 1, а высота - 2. Высота всего дерева равна 3.

Для деревьев часто удобно использовать следующее индуктивное определение.

Определение 1.11. Определим по индукции класс графов

, называемых деревьями. Одновременно для каждого из них определим выделенную вершину - корень.

1. Граф
   
   , с единственной вершиной
   
   и пустым множеством ребер
   
   является деревом (входит в
   
   ).
   Вершина
   
   называется корнем этого дерева.
2. Пусть графы
   
   с корнями
   
   принадлежат
   
   , а
   
   - новая вершина, т.е.
   
   . Тогда классу
   
   принадлежит также следующий граф
   
   , где
   
   ,
   
   . Корнем этого дерева является вершина
   
   .
3. Других графов в классе
   
   нет.

Рисунок 1.3 иллюстрирует это определение.


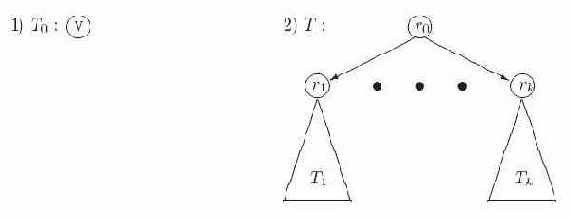
Рис. 1.3.  Индуктивное определение ориентированных деревьев

Определения ориентированных деревьев 1.10 и 1.11 эквивалентны.

Выделим еще один класс графов, обобщающий деревья, ациклические графы. Два вида таких размеченных графов будут использованы далее для представления булевых функций. У этих графов может быть несколько корней - вершин, в которые не входят ребра, и в каждую вершину может входить несколько ребер, а не одно, как у деревьев.

Дерево называется бинарным или двоичным , если у каждой его внутренней вершины имеется не более двух сыновей, причем ребра, ведущие к ним помечены двумя разными метками (обычно используются метки из пар: "левый" - "правый", 0 - 1, - и т.п.)

Бинарное дерево называется полным, если у каждой его внутренней вершины имеется два сына и все его ветви имеют одинаковую длину.


Содержание раздела

---

---

---

Главная сайта

---