Недетерминированные конечные автоматы и их детерминизация

Недетерминированные конечные автоматы, рассматриваемые в этом параграфе, являются обобщениями детерминированных: они при чтении очередного символа на входе могут выбрать в качестве следующего одно из нескольких состояний, а кроме того, могут изменить состояние без чтения входа. Основной результат, который мы установим, утверждает, что это обощение не существенно: недетерминированные и детерминированные конечные автоматы распознают одни и те же языки.

Определение 4.8. Недетерминированный конечный автомат (НКА) - распознаватель - это система вида

включающая следующие компоненты:

• ? ={a1, … , am} (m
  
  1) - конечное множество - входной алфавит;
• Q={q0, … , qn-1} (n
  
  1) - конечное множество - алфавит внутренних состояний;
• q0
  
  Q - начальное состояние автомата;
• F
  
  Q - множество принимающих (допускающих, заключительных) состояний;
• ?: Q ? (?
  
  {?})
  
  2Q - функция переходов.

Для a

? значение ?(q, a) - это множество состояний в каждое из которых может перейти автомат из состояния q, когда получает на вход символ a. ?(q, ?) - это множество состояний в каждое из которых может перейти автомат из состояния q без чтения символа на входе.

Как и для детерминированных автоматов, функцию переходов можно представить с помощью набора команд-программы: для каждой пары q

Q и a ? и каждого состояния q' ?(q, a) в программу помещается команда q a q', и для каждого состояния q' ?(q, ?) в программу помещается команда q q'. Отличие от детерминированного случая состоит в том, что для одной пары q Q и a ? в программе может быть несколько команд вида q a q' или не быть ни одной такой команды. Кроме того, могут появиться ?-команды (пустые переходы) вида q q', означающие возможность непосредственного перехода из q в q' без чтения символа на входе.

При табличном задании функции ? в таблице появляется (m+1)-ый столбец, соответствующий пустому символу ? и на пересечении строки q и столбца a

(? {?}) стоит множество состояний ?(q,a).

Для недетерминированного автомата M = <?, Q, q0, ? > в диаграмме DM=(Q, E) с выделенной начальной вершиной q0 и множеством заключительных вершин F ребра взаимно-однозначно соответствуют командам: команде вида q a

q' (a ?) соответствует ребро (q,q'), с меткой a , а команде вида q q' соответствует ребро (q,q'), с меткой ?.

Скажем, что заданный последовательностью ребер путь p=e1e2 … eT в диаграмме DM несет слово w=w1w2 … wt (t T), если после удаления из него "пустых" ребер (т.е. ребер с метками ?) остается последовательность из t ребер , метки которых образуют слово w , т.е. wi - это метка ребра . Очевидно, это эквивалентно тому, что последовательность меток на ребрах пути p имеет вид , где kj 0 (j=1,2, … , t+1) и .

Слово w переводит q в q' в диаграмме DM, если в ней имеется путь из q в q' который несет w .

На недетерминированные автоматы естественным образом переносится определение конфигураций и отношения перехода между ними.

Определение 4.9. Назовем конфигурацией НКА M = <?, Q, q0, F, ?, > произвольную пару вида (q, w), в которой q Q и w ?*. Определим отношение перехода из одной конфигурации в другую за один шаг:



или



Как и для ДКА, через обозначим рефлексивное и транзитивное замыкание отношения .

Внешне определение распознавания слов НКА совпадает с определением для ДКА.

Определение 4.10. НКА M распознает (допускает, принимает) слово w, если для некоторого \ .

Язык LM, распознаваемый НКА M, состоит из всех слов, распознаваемых автоматом:



Отличие состоит в том, что у НКА может быть несколько различных способов работы (путей вычисления) на одном и том же входном слове w. Считаем, что НКА распознает (допускает, принимает) это слово, если хотя бы один из этих способов приводит в заключительное состояние из F.

Из определения диаграммы DM непосредственно следует, что НКА M распознает слово w, тогда и только тогда, когда существует такое заключительное состояние q F, что в диаграмме DM слово w переводит q0 в q. Иными словами, в DM имеется путь из q0 в q, на ребрах которого написано слово w (с точностью до меток ?).

Пример 4.1. Рассмотрим НКА N1 = < {a, b}, {0,1,2,3, 4}, 0, {3}, ?>, где

?:Q\?Xab?

0	{0,1}	{0}
1			{4}
2	{3}
3			{1}
4		{2}

Его диаграмма представлена ниже на рис. 4.3.


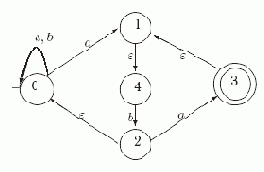
Рис. 4.3.  Диаграмма автомата N1

Рассмотрим работу этого автомата на слове ababa:





Так как 3 - заключительное состояние, то ababa LN1. Заметим, что у автомата N1 имеются и другие способы работы на этом слове, не ведущие к заключительному состоянию. Например, он может после чтения каждого символа оставаться в состоянии 0. Но чтобы слово допускалось, достаточно существовать хотя бы одному "хорошему" способу.

Очевидно, что детерминированные конечные автоматы являются частными случаями недетерминированных. Естественно спросить, распознают ли недетерминированные конечные автоматы больший класс языков чем детерминированные? Следующая теорема показывает, что классы языков, распознаваемых НКА и ДКА совпадают.

Теорема 4.2. (Детерминизация НКА)

Для каждого НКА M можно эффективно построить такой ДКА A, что LA = LM.

Доказательство Пусть M= <?, Q, q0, F, ? > - НКА. Процедура построения по нему эквивалентного ДКА состоит из двух этапов: на первом по M строится эквивалентный ему НКА M1, в программе которого отсутствуют переходы по ?, а на втором этапе по M1 строится эквивалентный ДКА A.


Содержание раздела

---

---