Построение сокращенных УБДР по формулам
Алгоритм СОКРАЩЕНИЕ-УБДР позволяет построить сокращенную УБДР для функции f, по любой другой ее УБДР. Но как построить УБДР, если f задана, например, с помощью формулы? Можно, конечно, попытаться построить полное бинарное дерево решений, объединить в нем все листья с меткой 0 в один сток, а листья с меткой 1 - в другой. Затем применить к получившейся УБДР алгоритм СОКРАЩЕНИЕ-УБДР. Но этот подход годится только для функций от небольшого числа переменных, так как полное БДР для f(x1, …, xn) будет содержать 2n листьев.
Другой подход связан с построением УБДР "сверху-вниз". Объясним его для естественного порядка переменных: x1< x2 < … < xn.
Начнем построение с корня, помеченного x1. Рассмотрим две остаточные функции: f0(x1, …, xn)=f(0, x2, …, xn) и f1(x2, …, xn)=f(1, x2, …, xn). Если они одинаковы, то f не зависит от x1 и тогда изменим метку у корня на x2. Если обе функции f0 и f1 существенно зависят от x2, то для каждой из них добавляем вершину, помеченную x2, и далее реализуем по индукции. Если fk (k

Пример 3.2. Рассмотрим, например, функцию f(x1, x2, x3, x4), заданную формулой (x1









Вначале создадим корень, помеченный x1, и рассмотрим остаточные функции, получающиеся при x1=0 и x1 =1. Имеем

Они разные и обе существенно зависят от x2. Поэтому добавим для каждой из них вершину, помеченную x2. Затем для каждой из них определим остаточные функции, получающиеся при x2=0 и x2 =1. Получим

Так как f00=f10, а f01 и f11 от x3 не зависят, то нам потребуется только одна вершина, помеченая x3. Она будет представлять функцию f00=f10=(x3

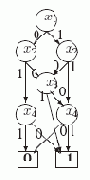
Рис. 3.6.
