Сумматор

Сумматором порядка n называют схему, вычисляющую результат сложения двух n-разрядных двоичных чисел

. Пусть

( здесь ai, bi, ci

{0, 1} - соответствующие двоичные разряды этих чисел).

Сумматор должен вычислять набор из (n+1)-ой результирующей функции:

задающих соответствующие разряды суммы c.

Обозначим через pi бит переноса из (i-1)-го разряда в i-ый. Тогда нетрудно видеть, что при i =0

c0 = a0 + b0 и p1 = a0

b0,

а при 1

n-1

ci= pi + ai + bi и pi+1 = (ai

bi)

(pi

ai)

(pi

bi).

Старший разряд c совпадает с последним переносом: cn=pn.

Рассмотрим теперь построенную выше схему S+ как схему, вычисляющую набор из двух функций: x

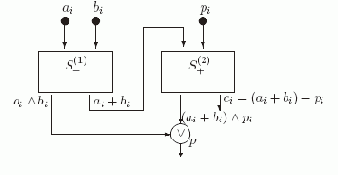
y (в вершине a) и x+y (в вершине d). Используя два экземпляра этой схемы S+(1) и S+(2), можно легко реализовать схему одноразрядного сумматора SUM1 (см. рис. 2.4) , которая имеет три входа ai, b_ i и pi (1

n-1) и вычисляет ci и pi+1.

Рис. 2.4. Схема SUM1

Действительно, из построения следует, что в вершине p этой схемы вычисляется функция fp = (ai

bi)

((ai + bi)

pi) = (ai

bi)

(pi

ai)

(pi

bi) = pi+1. Из представленной схемы видно, что сложность одноразрядного сумматора L(SUM1)= 9.

Теперь из S+ и одноразрядных сумматоров SUM1 соберем схему SUMn для n-разрядного сумматора.

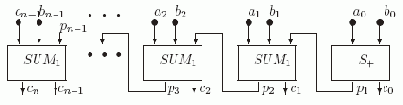
Рис. 2.5. Схема cумматора SUMn

Таким образом мы установили следующее утверждение.

Теорема 2.3.

Для каждого n

1 cуществует схема SUM, реализующая операцию суммирования двух n-разрядных двоичных чисел и имеющая сложность L(SUMn)= 9n -5.

Замечание Логические схемы интенсивно исследовались 50-х-70-х годах прошлого столетия. В частности, К. Шеннон и О.Б. Лупанов установили оценки сложности схем для булевых функций от n аргументов. Оказалось, что любую такую функцию можно реализовать со сложностью не большей (по порядку) 2n/n и что "почти все" они имеют не меньшую сложность. При этом до сих пор не известна ни одна последовательность "конкретных" функций fn, сложность которых по порядку превосходила бы линейную функцию.

Содержание раздела