Рассмотрим схему S+ на рис.
Рассмотрим схему S+ на рис. 2.2.
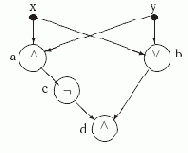
Рис. 2.2. Схема S+ для функции x+y
В соответствии с определением вершины этой схемы реализуют следующие функции:
fa(x,y) = x







Таким образом, схема S+ реализует (в вершине d) функцию + сложения по модулю 2.
Из приведенного выше примера следует, что L(S+)=4 и L(+)

Используя схему S+, нетрудно построить схему Sodd для реализации линейной функции-суммы n аргументов по модулю 2 odd(X1,X2,…, Xn)= X1 +X2 +… + Xn (см. рис. 2.3).
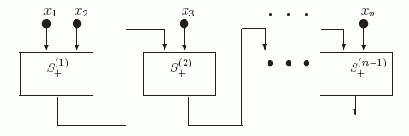
Рис. 2.3. Схема Sodd
На этой схеме прямоугольники S+(1), S+(2), … ,S+(n) содержат копии схемы S+. При этом входами S+(1) являются переменные x1 и x2, а входами S+(i+1) являются выход схемы S+(i) и переменная xi+1. По индукции легко показать, что вершина d в S+(i) реализует функцию (x1 + x2 + … + xi+1). Таким образом, нами установлена
Теорема 2.2.
Существует схема Sodd, реализующая функцию odd(X1,X2,…, Xn)= X1 +X2 +… + Xn
со сложностью L(Sodd)= 4 (n-1).
