Логические схемы (схемы из функциональных элементов)

Многие элементы в современной электронике являются устройствами, преобразующими некоторые входные сигналы (данные) в выходные. Логические схемы, в отечественной литературе чаще называемые схемами из функциональных элементов, представляют собой математическую модель таких устройств, в которых временем выполнения преобразования входов в выходы можно пренебречь.

Чтобы не усложнять определение, зафиксируем конкретный базис B0={

, , ¬} и определим схемы в этом базисе.

Определение 2.1. Логической схемой (схемой из функциональных элементов) в базисе B0 называется размеченный ориентированный граф без циклов S=(V,E), в котором

1. вершины, в которые не входят ребра, называются входами схемы, и каждая из них помечена некоторой переменной (разным вершинам соответствуют разные переменные);
2. в каждую из остальных вершин входит одно или два ребра; вершины, в которые входит одно ребро помечены функцией ¬, а вершины, в которые входят по два ребра, - одной из функций
   
   или
   
   . Такие вершины называются функциональными элементами.

Как и для деревьев, для ориентированных графов без циклов можно естественным образом ввести понятие глубины.

Определение 2.2. Глубина вершины v

V в схеме S=(V,E) - это максимальная длина пути из входов S в v .

Глубиной D(S) схемы S назовем максимальную из глубин ее вершин.

Пусть входы схемы S помечены переменными x1, … , xn. С каждой вершиной v

V схемы S свяжем булеву функцию fv(x1,… , xn), реализуемую в этой вершине. Определим fv индукцией по глубине v .

Определение 2.3.

Базис: v имеет глубину 0. Тогда это входная вершина, которая помечена некоторой переменной xi. Положим fv(x1,… , xn) = xi.

Шаг индукции. Пусть всем вершинам w глубины

k уже сопоставлены функции fw и пусть v - произвольная вершина глубины k+1. Тогда

• если v помечена ¬ и в нее входит ребро (w,v) , то положим

  

• если v помечена

  
  и в нее входят два ребра (w1,v) и (w2,v), то положим
  

• если v помечена

  
  и в нее входят два ребра (w1,v) и (w2,v), то положим
  

Нетрудно понять, что шаг индукции в этом определении корректен, так как, если в схеме S имеется ребро (w,v) и глубина вершины v равна k+1, то глубина вершины w не превосходит k и для нее fw уже определена по индукционному предположению.

Определение 2.4. Схема S реализует набор булевых функций g1, g2, … , gm, если для каждого i [1,m] в схеме существует такая вершина vi, что .

Замечание. Определение логических схем естественным образом можно распространить и на другие базисы. При этом, однако, для вершин, помеченных несимметричными функциями ( например, импликацией), нужно явно нумеровать входящие в них ребра, указывая, каким аргументам они соответствуют.

Определение 2.5. Сложность L(S) схемы S - это число функциональных элементов в S. Сложность L(f) булевой функции f(x1, …, xn) - это наименьшая из сложностей схем, реализующих эту функцию.

Отношения между булевыми функциями и схемами естественно приводят к двум следующим основным проблемам.

Проблема анализа: по заданной схеме из функциональных элементов и выделенному подмножеству ее выходных вершин определить булевы функции, реализуемые в этих вершинах.

Проблема синтеза: по некоторому описанию булевой функции построить схему из функциональных элементов, реализующую эту функцию. При решении проблемы синтеза для исходной функции часто стараются построить схему минимальной или почти минимальной сложности.

Пример 2.1. Рассмотрим схему S1

с тремя входными переменными x, y и z, изображенную на рис. 2.1 и решим для нее проблему анализа.


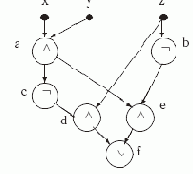
Рис. 2.1.  Схема S1

В соответствии с данным выше определением вершины схемы S1 реализуют следующие функции:

fa(x,y,z) = x y, fb(x,y,z) = ¬ z, fc(x,y,z) = ¬ fa(x,y,z)=¬( x y), fd(x,y,z) = fc(x,y,z) z = ¬( x y) z, fe(x,y,z) =fa(x,y,z) fb(x,y,z)= x y ¬ z и, наконец, ff(x,y,z) =fd(x,y,z) fe(x,y,z) = (¬( x y) z) ((x y ) ¬ z).

Глубина этой схемы D(S1)= 4, а ее сложность L(S1)=6. В то же время формула для результирующей функции ff содержит 7 функциональных знаков. За счет чего достигнута экономия? За счет того, что функция (x y) в схеме S1 вычисляется один раз в вершине a, а в формуле приходится вычислять ее дважды.

В этом и состоит основное преимущество вычислений булевых функций схемами: каждую подформулу (подфункцию) достаточно вычислить один раз, а затем полученное значение можно использовать сколько угодно раз в качестве аргумента для других подфункций.


Содержание раздела

---

---