Виброзащита машин и механизмов
|
Краткое содержание: Виброзащита машин и механизмов. Методы виброзащиты. Взаимодействие двух подвижных звеньев. Подрессоривание и виброизоляция. Динамическое гашение колебаний. Трение в механизмах. Виды трения. Силы в кинематических парах с учетом трения. Силовой расчет механизмов с учетом сил трения. Понятие о КПД механической системы. КПД механической системы при последовательном и параллельном соединении механизмов. Приложение: Метод планов положений, скоростей и ускорений при анализе простейшего кулисного механизма.
Виброзащита в машин и механизмов.
Как отмечалось ранее, при движении механической системы под действием внешних сил в ней возникают механические колебания или вибрации. Эти вибрации оказывают влияние на функционирование механизма и часто ухудшают его эксплуатационные характеристики: снижают точность, уменьшают КПД и долговечность машины, увеличивают нагрев деталей, снижают их прочность, оказывают вредное воздействие на человека-оператора. Для снижения влияния вибраций используют различные методы борьбы с вибрацией. С одной стороны при проектировании машины принимают меры для снижения ее виброактивности (уравновешивание и балансировка механизмов), с другой - предусматриваются средства защиты как машины от вибраций, исходящих от других машин (для рассматриваемой машины от среды), так среды и операторов от вибраций данной машины.
Методы виброзащиты.
Существующие виброзащитные устройства по методу снижения уровня вибраций делятся на:
- динамические гасители или антивибраторы, в которых опасные резонансные колебания устраняются изменением соотношения между собственными частотами системы и частотами возмущающих сил;
- виброизоляторы, в которых за счет их упругих и демпфирующих свойств уменьшается амплитуда колебаний как на резонансных и нерезонансных режимах.
Взаимодействие двух подвижных звеньев.

Рассмотрим механическую систему (рис. 9.1), состоящую из двух подвижных звеньев, образующих между собой кинематическую пару.
Для упрощения предположим, что движение звеньев возможно только по одной координате x. Масса первого звена m1 , второго - m2 . На звено 2 действует периодическая внешняя сила F2 = F20
*sin wt , действием сил веса принебрегаем Уравнения движения звеньев

С учетом F21 = - F12, определим реакцию в точке контакта между звеньями
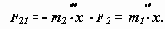
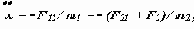
F21 (m1 + m2)/(m1+ m2) = - F2 / m2 ,
F21 = - F2* m1 / (m1 + m2).
Проанализируем эту зависимость:
если m1 => 0, то F21 => 0 ; если m2=> 0 , то F21 => F2 ;
если m2 = m1 = m , то F21 => - 0.5*F2 ;
если m2 =>? , то F21 => 0 ;
eсли m1 => ? , то F21 => - F2 .
Анализ показывает, что реакция взаимодействия между звеньями зависит от соотношения их масс и величины внешней силы. При этом кинетическая энергия системы
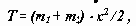
Подрессоривание или виброизоляция.

В этой механической системе x2 >x1 ( предположим, что x2 >x1 ) и D x = x2 - x1 , тогда кинетическая энергия системы
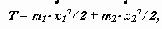
U = c* D x2 / 2.
То есть в системе с виброизолятором только часть работы внешней силы расходуется на изменение кинетической энергии. Часть этой работы переходит в потенциальную энергию упругого элемента и часть рассеивается демпфером (переходит в тепло и рассеивается в окружающей среде).
Уравнения движения


Динамическое гашение колебаний.
Динамические гасители или антивибраторы широко применяются в машинах работающих в установившихся режимах для отстройки от резонансных частот (например, в судовых двигателях внутреннего сгорания).
Динамические гасители могут быть выполнены в виде упругого или физического маятника. Рассмотрим простейший линейный упругий динамический гаситель (рис.9.4). Принцип действия динамического гасителя заключается в создании гасителем силы направленной противоположно возмущающей силе. Настройка динамического гасителя заключается в подборе его собственной частоты: собственная частота гасителя должна быть равна частоте тех колебаний, амплитуду которых необходимо уменьшить (“погасить”)
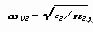
Уравнения движения системы с динамическим гасителем, схема которого изображена на рис. 9.4



Трение в механизмах. Виды трения.
Способность контактирующих поверхностей звеньев сопротивляться их относительному движению называется внешним трением. Трение обусловлено неидеальным состоянием контактирующих поверхностей (микронеровности, загрязнения, окисные пленки и т.п.) и силами межмолекулярного сцепления. Трение в кинематических парах характеризуется силами трения и моментами сил трения. Силой трения называется касательная составляющая реакции в КП (составляющая направленная по касательной к контактирующим поверхностям), которая всегда направлена против вектора скорости относительного движения звеньев.
Различают следующие виды трения:
- трение покоя проявляется в момент, когда два тела находящиеся в состоянии относительного покоя начинают относительное движение (касательную составляющую возникающую в зоне контакта до возникновения относительного движения, в условиях когда она меньше силы трения покоя, будем называть силой сцепления; максимальная величина силы сцепления равна силе трения покоя);
- трение скольжения появляется в КП при наличии относительного движения звеньев; для большинства материалов трение скольжения меньше трения покоя;
- трение качения появляется в высших КП при наличии относительного вращательного движения звеньев вокруг оси или точки контакта;
- трение верчения возникает при взаимодействии торцевых поверхностей звеньев вращательных КП (подпятники).


Fтр ij = f ? F nij ,
где f - коэффициент трения скольжения .
Силы в кинематических парах с учетом трения.
1. Поступательная КП (рис.9.7).

- реактивный момент Mij ,
- величина реакции Fij ;
- направление вектора Fij ;
Полная величина реакции в КП равна векторной сумме

Если tg j » f => 0, то Fij => F nij , т.е. к решению без учета трения.
Число неизвестных в поступательной КП при силовом расчете с учетом трения увеличилось и равно ns = 3.
2. Вращательная КП Силовой расчет с учетом трения является моделью КП более высокого уровня, с большей степенью приближения модели к реальной КП. При этом известны геометрические размеры элементов КП (радиусы цапф) и коэффициент трения скольжения. Так как в реальных парах имеются зазоры, то на расчетной схеме (рис.9.8) пару представляют как высшую.

- направление реакции Fij ;
- величина реакции Fij ;
- величина силы трения Fтр ij;
Момент трения в КП


- величина реакции Fij ;
- направление реакции Fij ;
- момент сил трения Мтрij
- точка приложения силы - точка контакта рабочих профилей кинематической пары С2вп;
- направление нормальной составляющей Fnij - контактная нормаль к профилям (размеры и форма профилей заданы);
- направление тангенциальной составляющей Fтрij - касательная к профилям в точке контакта;
- коэффициенты трения качения k и скольжения f.

Число неизвестных в высшей КП при силовом расчете с учетом трения увеличилось с ns = 1 до ns = 3 ( так как в паре имеется два вида трения).
Силовой расчет механизмов с учетом сил трения.
Постановка задачи силового расчета: для исследуемого механизма при известных кинематических характеристиках и внешних силах, а также размерах элементов КП и величинах коэффициентов трения в них, определить уравновешивающую силу или момент (управляющее силовое воздействие) и реакции в кинематических парах механизма.
Методы решения задач силового расчета с учетом трения :
- составление общей системы уравнений кинетостатики с уравнениями для расчета сил и моментов сил трения с числом уравнений соответствующим числу неизвестных;
- метод последовательных приближений: на первом этапе решается задача кинетостатического расчета без учета трения и определяются нормальные составляющие реакций, по ним рассчитываются силы трения и определяются реакции с учетом трения.
Понятие о КПД механической системы.
Коэффициентом полезного действия или КПД механической системы называют отношение работы сил полезного сопротивления к работе движущих сил за цикл ( или целое число циклов ) установившегося режима работы.
КПД механизма характеризует его эффективность при преобразовании энергии, определяет соотношение полученной на выходе полезной энергии и энергетических потерь в механизме на трение, перемешивание масла, вентиляцию, деформацию звеньев и др. Величину КПД можно рассчитать по следующей зависимости:

h = 1 - | Aпот/ Ai | = 1 - y , где Ai - работа движущих сил, Aj - работа сил полезного сопротивления, h - коэффициент полезного действия, y - коэффициент потерь.
Работа движущих сил за цикл


j in ,j jn и j i0 , j j0 - значения угловых координат звеньев i и j ,соответственно в начале и в конце цикла.
Подставим эти выражения в формулу для КПД и получим
h = | Aj /Ai | = | Мcср *D j j | / | Мдср*D j i | = | Мcср | / | Мдср | ,
где uji - передаточное отношение механизма.
КПД механической системы при последовательном и параллельном соединении механизмов.
- при последовательном соединении (рис. 9.11) весь поток механической энергии проходит последовательно через каждый из механизмов


-
1. Теория механизмов и машин. Под ред. К.В.Фролова. М.: Высшая школа, 1987.
- Левитский Н.И. Колебания в машинах: Учебное пособие для втузов. - М: Наука. Гл. ред. физ. - мат. лит., 1988. - 336 с.
- Штейнвольф Л.И. Динамические расчеты машин и механизмов. - Москва - Киев: Машгиз., 1961. - 340 с.
- Вибрации в технике: Справочник. В 6-ти т./ Ред. совет: В.Н.Челомей и др.,- М.: Машиностроение, 1981. - Т.6, Защита от вибрации и ударов/ Под ред. К.В.Фролова, 1981. - 456с.
- Силовой расчет, уравновешивание, проектирование механизмов и механика манипуляторов: Учебное пособие. Под ред. А.К.Мусатова. М.: Изд. МГТУ, 1990.

