Режимы движения машины
|
Краткое содержание: Режимы движения машины. Режим движения пуск-останов. Определение управляющих сил по параметрам движения при пуске и останове. Алгоритм решения прямой задачи динамики при неустановившемся режиме движения машины.
Режимы движения машины.
В зависимости от того какую работу совершают внешние силы за цикл движения машины различают три режима движения: разгон, торможение и установившееся движение. Циклом называют период времени или период изменения обобщенной координаты через который все параметры системы принимают первоначальные значения.

- Разгон => Адц > Асц , Аa ц > 0;
- Установившееся движение => Адц = Асц , Аa ц = 0;
- Торможение (выбег) => Адц Асц , Аa ц 0.
Режим движения "пуск - останов".
Существует большое количество машин и механизмов: гидроподъемники, манипуляторы, механизмы управления метательными аппаратами, механизмы шасси, механизмы автоматических дверей и многие другие, исполнительное звено которых перемещается из начального положения в конечное. При этом в начале и в конце цикла движения исполнительное звено неподвижно. Такой режим движения механизма называется режимом "пуск-останов". Механизм начинает движение из состояния покоя, в конце цикла выходное звено механизма должно остановиться и зафиксироваться в заданном положении. Возможны три варианта остановки выходного звена:
- остановка с жестким ударом (рис.7.2) w 1n > 0, e 1n стремиться к бесконечности ;
- остановка с мягким ударом (рис. 7.3 ) w 1n = 0, e 1n не равно 0 .
Для динамической модели в конечном положении

безударная остановка или остановка с удержанием в конечном положении (рис. 7.4) w 1n = 0, e 1n = 0 .
В этом случае к рассмотренному выше условию w 1n = 0 , добавляется условие e 1n = 0. Для динамической модели в конечном положении
e 1n = dw 1n/dt = М прa n / Iпрa n - w 1n2/(2* Iпрa n) * (d Iпрa n /dj 1),
Если w 1n = 0, Iпр > 0, то e 1n = 0 при М прa n = 0.
Таким образом при остановке с мягким ударом необходимо выполнить условие
w 1n = 0 => Аa n = 0;
при безударной установке и фиксации объекта в конечном положении нужно выполнить одновременно два условия
w 1n = 0 => Аa n = 0;
e 1n = 0 => М прa n = 0.


Типовые диаграммы движущей силы.

Гидроподъемник поворачивает платформу - звено 1 на заданный угол D j 1, при этом центр масс S1 поднимается на высоту HS1 под воздействием силы давления в гидроцилиндре Fд , закон изменения которой за цикл определяется одной из диаграмм, изображенных на рис. 7.5.

k * abs (Мпрс 0 ) = Мпрд 0 ,
где k = 1.05 ... 2 - коэффициент запаса по моменту для разгона системы.
Раскрывая это уравнение, получим


abs (Мпрс n ) = Мпрд n .
Раскрывая это уравнение, получим


Аa n = 0, Ад n = abs ( А cn );
- для диаграммы движущей силы, изображенной на рис. 7.5 а
- для диаграммы движущей силы, изображенной на рис. 7.5 б
Fд 0 * a
* HD + 0.5* ( Fд 0 + Fд * ) * ( b
- a
)* HD + 0.5* ( Fд *+ Fд n )* ( 1 - b
) * HD =
= G1 * HS1 ,
Fд * = G1 * HS1 - [Fд 0 * a + 0.5* Fд 0 * ( b - a ) + 0.5* Fд n* ( 1 - b ) ] /
/ { 0.5* [( b - a ) + ( 1 - b )]* HD }.
Fд 0 * a * HD + Fд * * ( b - a )* HD + Fд n * ( 1 - b ) * HD = G1 * HS1 ,
Fд * = G1 * HS1 - [ Fд 0 * a + Fд n * ( 1 - b )] * HD / [( b - a )* HD ].
В отличие от установившегося режима движения режимы разгона и торможения называются неустановившимися. К этому режиму относят и режим движения "пуск-останов". Прямая задача динамики: определение закона движения машины при заданных внешних силовых воздействиях ( как сил и моментов сопротивления, так и движущих или управляющих сил ). Эта задача относится к задачам анализа, при которых параметры механизмов заданы, либо могут быть определены на предварительных этапах расчета. Для простоты и наглядности рассмотрим алгоритм решения этой задачи на примере конкретного механизма гидроподъемника. По условиям функционирования гидроподъемник за цикл движения должен переместить платформу 1 (рис. 7.6) на угол D j 1 и зафиксировать ее в конечном положении. При этом силы сопротивления определяются силами веса платформы и звеньев гидроцилиндра, движущие силы - давлением жидкости в цилиндре.
Алгоритм решения прямой задачи динамики при неустановившемся режиме .
Постановка задачи .
Дано: Кинематическая схема механизма и его размеры
lAB = 1 м, lBS1 = 2 м, lBD = 0.7м, lAC = 1.45м,
lBS2 = 0.35м, lBS3 = 0.4 м;
массы и моменты инерции звеньев m1 = 1000 кг,
IS1 = 800 кг * м 2, m2 = 50 кг, IS2 = 2 кг * м 2, m3 = 100 кг,
IS3 = 5 кг * м 2; w 1нач = 0, D j 1 = 30° , j 1нач = 0.
____________________________________________
Определить: w 1 = f(j 1 ), t = f(j 1 ), w 1 = f( t ), e 1 = f(j 1 ).
1. Выбор динамической модели и определение ее параметров.

1.1. Определение кинематических передаточных функций для звеньев механизма u21 = u31 , центров масс VqS1 , VqS2 и VqS3 и точки приложения движущей силы VqD . Для определения этих функций воспользуемся методом проекций векторного контура механизма .

l AB = l AC + l CB;
l AD = l AB + l BD;
l AS2 = l AC + l CS2;
l AS3 = l AC + l CS3;
l AS1 = xS1 + yS1 .
Для первого векторного контура l AB = l AC + l CB проекции на оси координат
lAB * cos j 1 = xC + lCB * cos j 2 ,
lAB * sin j 1 = yC + lCB * sin j 2 ,
j 2 = arctg [( lAB * sin j 1 - yC )/( lAB * cos j 1 - xC )].
Производные от этих выражений по j 1
- lAB * sin j 1 = VqCB * cos j 2 - lCB * u21* sin j 2 ,
lAB * cos j 1 = VqCB * sin j 2 + lCB * u21* cos j 2 ,
позволяют определить первые передаточные функции
u21 = lAB* ( sin j 1* tgj 2 + cos j 1 )/ [ lCB* ( sin j 2* tgj 2 + cos j 2 )],
VqCB = - lAB* ( sin j 1 - cos j 1 * tgj 2)/ ( sin j 2* tgj 2 + cos j 2 ).
Для второго векторного контура l AD = l AB + l BD проекции на оси координат
xD = xB + lBD * cos (j 2 + p ),
yD = yB + lBD * sin (j 2 + p ) .
Производные от этих выражений по j 1
VqDx = VqBx - lBD * u21* sin (j 2 + p ),
VqDy = VqBy + lBD * u21* cos (j 2 + p ) ,
позволяют определить первую передаточную функцию
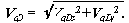
xS2 = xB + lBS2 * cos (j 2 + p ),
yS2 = yB + lBS2 * sin (j 2 + p ) .
Производные от этих выражений
VqS2x = VqBx - lBS2 * u21* sin (j 2 + p ),
VqS2y = VqBy + lBS2 * u21* cos (j 2 + p ) ,
позволяют определить первую передаточную функцию
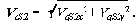
xS3 = xС + lBS3 * cos j 2 ,
yS3 = yС + lBS3 * sin j 2 .
Производные от этих выражений
VqS3x = - lС S3 * u21* sin j 2 ,
VqS3y = lCS3 * u21* cos j 2 ,
позволяют определить первую передаточную функцию
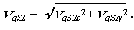
xS1 = lAS1 * cos j 1 ,
yS1 = lAS1 * sin j 1 .
Производные от этих выражений по j 1
VqS1x = lAS1 * sin j 1 ,
VqS1y = lAS1 * cos j 1 ,
позволяют определить первую передаточную функцию
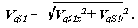

Расчет проведем для закона изменения движущей силы, который изображен на рис.7.5. Величина движущей силы в начальном положении механизма рассчитывается по формуле

Fд0 = 1.1* abs (10000* 2 + 500* 0.97 + 1000* 0.0342)/ 0.967 = 23341.3 Н.
В конечном положении величина движущей силы рассчитывается по формуле:

Значение движущей силы в интервале ( b - a )* HD определим по формуле:
Fд * = {abs( G1 * HS1 + G2 * HS2 + G3 * HS3 )-
- [ Fд 0 * a + Fд n * ( 1 - b )] * HD} / [( b - a )* HD ].
HS1 = yS1n - yS10 = 1 - 0 = 1 м; HS2 = yS2n - yS20 = 0.162 - (-0.338) = 0.5 м;
HS3 = yS3n - yS30 = -0.364 - (-0.364) = 0;
подставим полученные значения в формулу и получим
Fд * = {abs( 10000*1+ 500*0.5 + 1000*0)- [23341.3*0.32 + 18325.7*
*(1 - 0.65 )]*0.518}/[( 0.65 - 0.32 )* 0.518] = (10250 - 7191)/0.171 = 17889 Н .



- 2. определение приведенного суммарного момента сил сопротивления В нашем примере силами сопротивления являются силы веса звеньев механизма, поэтому расчет суммарного приведенного момента сил сопротивления проводим по формуле


1.4. Определение суммарного приведенного момента инерции
В рассматриваемом механизме приведенный момент инерции суммируется из масс и моментов инерции звеньев и может быть рассчитан по следующей зависимости



Iпрa c = m1 * (VqS1)2 + IS1 = 1000 * (2)2 + 800 = 4800 кг * м 2 .
Суммарный приведенный момент инерции и равен сумме постоянной и переменной частей
Iпрa = Iпрa c + Iпрa v .
2. Определение суммарной работы внешних сил.
Суммарную работу внешних сил получим интегрированием суммарного приведенного момента Мпрa по обобщенной координате dj 1
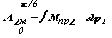
tg y 1 = yMпрa 1ср / k1 = yD Aa 1 / xD j 1 ,
или m М * M прa 1ср / k1 = m A * D Aa 1 / m j * D j 1 ,
так как M прa 1ср = D Aa 1 / D j 1 , то m A= m М * m j / k1 .
Графики, иллюстрирующие построение диаграммы работы, приведены на рис.7.1 6 и 7.1 7
3. Определение угловой скорости звена приведения
Определение закона движения звена приведения в виде диаграммы изменения угловой скорости в функции обобщенной координаты w 1= f(j 1) проводится по формуле



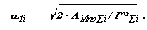

4. Определение времени цикла.
Время цикла определяется по диаграмме t= f (j 1). Для построения этой диаграммы проведем интегрирование диаграммы угловой скорости

tg y 1 = k2 / yw 1ср1 = yD t1 / xD j 1 ,
или k1 /m w * w 1ср 1 = m t * D t1 / m j * D j 1 ,
так как 1/ w 1ср 1 = D t1 / D j 1 , то m w = k2* m j / m w .
5. Построение диаграммы угловой скорости в функции времени
Диаграмма угловой скорости w 1 = f ( t ) в функции времени строится по диаграммам w 1 = f (j 1 ) и t= f (j 1 ), исключением переменной j 1 .



Для расчета углового ускорения звена приведения e 1 = f(j 1) можно воспользоваться двумя различными зависимостями:
а). e 1 = dw 1 /dt = dw 1/dj 1 * dj 1/dt = w 1 * dw 1/dj 1 ,
б). e 1 = dw 1/dt = М прa / Iпрa - w 12/(2* Iпрa ) * (d Iпрa /dj 1).
Применение первой формулы приводит к большим погрешностям, так как она основывается на использовании одной из конечных зависимостей расчета w 1 = f (j 1 ). Кроме того, в точках с нулевыми значениями w 1расчет по этой формуле дает неверный результат e 1 = 0. Поэтому проведем расчет зависимости e 1 = f(j 1) по второй формуле .Диаграмма функции e 1 = f(j 1) приведена на рис. 7.22.

При определении в формуле углового ускорения производной d Iпрa /dj 1 часто используется метод поднормали. На графике дифференцируемой функции (рис. 23) в рассматриваемой точке проводят касательную t - t , нормаль n - n и ординату yIпрa i . Измеряют отрезок xi между точками пересечения с осью x ординаты и нормали. Рассчитывают производную с учетом масштабов по осям по формуле



