Архитектуры ротационных БД
Сервер отсутствует. На рис. 2.1 представлена временная диаграмма работы (в начальный момент) ротационной базы данных в ЛВС, в составе которой отсутствует сервер. Сеть содержит n рабочих станций, по числу которых БД разбита на n сегментов.

Рис. 2.1. Ротация сегментов БД
Круговая шкала времени отображает один цикл полной ротации сегментов, т.е. суммарное время однократного пребывания всей БД на одной рабочей станции. Цикл разбит на n равных отрезков времени длительностью T0. Это — такт системы, в течение которого каждая РС связана с одним сегментом БД. Время длительности такта T0 состоит из собственно времени Tдост
активного доступа к сегменту БД, пребывающему в данный момент в памяти РС, и времени ротации tрот, в течение которого производится смена сегмента в памяти РС с помощью сетевой ОС при невозможности доступа пользователя, T0 = Tдост + tрот. Таким образом, можно говорить о коэффициенте kдост доступности сегмента БД, определяющего долю времени длительности такта T0, в течение которого пользователь имеет доступ к сегменту, пребывающему в памяти РС,

Рассмотренная схема в наибольшей степени соответствует ЛВС с организованным круговым одновременным обменом между рабочими станциями по принципу "соседу слева (справа)".
Заметим, что передача по принципу общей шины приводит к разделению времени обмена. Однако и в этом случае есть простой выход — в асинхронном пребывании сегментов в памяти РС. В этом случае ротация сегментов производится последовательно между парами РС по кругу, а каждый вновь поступивший на РС сегмент до удаления прежнего сегмента находится в специальном буфере.
Такая, с учетом работы общей шины, ротация представлена на рис. 2.2.

Рис. 2.2. Ротация сегментов по общей шине
При этом необходим компромисс между временем последовательного обмена внутри каждой пары РС и длительностью T0 пребывания сегмента на отдельной РС. Так как T0 в ЛВС с "шинной архитектурой" может существенно возрасти, это, как будет видно далее, приведет к увеличению среднего времени ожидания сегментов на РС в случае поступления к ним запросов.
Обращаем внимание на то, что рассмотренные схемы ротации с последовательным доступом к каждому сегменту предполагают возможность выполнения таких запросов, по которым вносятся изменения в БД. Дополнительная синхронизация доступа к БД в этом случае не требуется.
Кольцевая схема ротации с сервером. Наличие сервера (рис. 2.3) в ЛВС при той же кольцевой схеме ротации, благодаря существенно большему объему памяти, позволяет значительно увеличить количество сегментов, "блуждающих" в сети, сделав их число независящим от числа рабочих станций.

Рис. 2.3. Ротационная БД с сервером
Кроме того, сервер позволяет разнообразить дисциплины ротации. Он допускает такое решение, при котором цикл ротации отдельных сегментов может изменяться, быть разным для разных сегментов, исключать сегменты из ротации вообще, организовывать архивы и т.д.
Ротационная БД в ЛВС типа "звезда". Работа БД представлена на рис. 2.4.

Рис. 2.4. БД в ЛВС типа "звезда"
ЛВС типа "звезда" реализует все достоинства ранее рассмотренной ЛВС с сервером и позволяет их развить. Это развитие заключается в следующем.
Оперативно реализуется переменная структура ЛВС, так как рабочие станции легко могут исключаться "из обращения", а также могут включаться дополнительные станции.ЛВС становится в большей степени управляемой. В частности, в процессе работы пользователя некоторые запросы могут приводить к длительному времени отсутствия новых запросов. Например, при работе с затребованной литературой, архивными материалами и т.д.На это время целесообразно исключить РС из процесса ротации, ускорив работу других РС. Такая возможность может быть учтена либо сервером, либо самим пользователем. В последнем случае он получает возможность "включаться" в БД, если ему это необходимо, либо "выключаться" из нее. Тем самым он увеличивает производительность своего компьютера.
Временной режим работы обусловлен периодическим обменом сегментами БД "сервер

Эффективность и технические требования
В общем случае, при вхождении сервера в состав ЛВС и при разбиении БД на m сегментов, при котором m > n (n — число рабочих станций), вероятность нахождения сегмента на одной из РС в процессе ротации равна


Схема на рис. 2.3 соответствует случаю m = n.
Тогда среднее время Tож ожидания нужного сегмента, то есть возможного начала обращения к нужному сегменту на той РС, которая выработала запрос, находится на основе вероятности того, что он поступит через один такт, через два такта и т.д. Максимальное число учитываемых тактов равно m - 1:
 |
(2.1) |
Тогда полное время обслуживания запроса в ротационной БД находится следующим образом:
 |
(2.2) |
где tобсл — время выполнения запроса с помощью СУБД.
Сравним это полное время обслуживания со средним временем обслуживания T*обсл "традиционной" БД, реализованной на сервере. Напомним, что при обслуживании такой БД многоканальная система массового обслуживания, где множество рабочих станций обеспечивают массовый доступ, реально, с помощью одноканальной СУБД, на этапе обслуживания потока заявок преобразуется в одноканальную систему массового обслуживания с неограниченной очередью.
Допустив, что время выполнения запроса с помощью СУБД в данном случае совпадает с тем же временем в ротационной БД (ротация не предполагает каких-либо принципиальных изменений "традиционных", известных, широко применяемых СУБД), получим:
 |
(2.3) |
где ? — известное отношение


Уточним, что ?* = n?польз, где ?польз — интенсивность потока запросов с одной РС при данной организации БД. Однако здесь мы пренебрегли временем передачи сообщений в ЛВС, учитывая существенный характер ограничений другого рода. А именно, суммарная интенсивность ?* потока запросов в системе должна быть ограничена значением, обеспечивая соотношение ? < 1. Полное время обслуживания T*обсл значительно возрастает при значениях ?, близких единице:
T*обсл

?

В ротационной базе данных каждая РС независимо от других реализует одноканальную систему массового обслуживания с неограниченной очередью, где, несомненно, тоже должно выполняться соответствующее ограничение ?польз < ?польз, где ?польз — интенсивность запросов пользователя с одной РС, ?польз
— интенсивность обслуживания запросов пользователя с одной РС,

 | (2.4) |
Таким образом, исследуя вопрос о целесообразности построения ротационной БД, необходимо изучить практические возможности обеспечения таких характеристик ЛВС, их аппаратных и программных средств, при которых выполняется соотношение

или
 | (2.5) |

Напоминаем, что здесь
T0 — время (длина) такта системы,
m — число сегментов БД,
n — число рабочих станций ЛВС,
tобсл — время выполнения одного запроса СУБД (характеристика используемой системы управления базой данных),
?польз — интенсивность потока запросов одного пользователя,
? — интенсивность обслуживания запросов данной СУБД.
Однако выражение (2.5) получено в предположении, что заявка на обслуживание, поступившая от конкретной РС к некоторому сегменту si, не претерпевает какого-либо влияния возможных, в достаточно близкое время, заявок, пришедших к этому же сегменту от других РС "на пути следования" сегмента к данной РС. А именно, за предполагаемое среднее время Tож требуемый сегмент может быть "перехвачен" другой РС, "предшествующей" ожидающей.
При значительной интенсивности ? заявок такой возможностью нельзя пренебречь.
Предположим не более чем однократную возможность такого "перехвата".
Тогда, считая, что поток заявок к БД простейший (пуассоновский, экспоненциальный), вероятность Pi того, что сегмент si без дополнительных помех на пути следования дойдет до данной РС, находится как
 | (2.6) |

Если запросы ко всем сегментам равновероятны, то
 | (2.7) |
 | (2.8) |
"Перехват" дополняет общее время выполнения заявки составляющей (1-P)tобсл. Тогда окончательно среднее время обслуживания заявок в ротационной БД в рассматриваемом случае определяется как
 | (2.9) |
 | (2.10) |
Многосерверные сетевые БД с циркулирующей информацией
Рассмотрим локальную вычислительную сеть, которая работает по принципу "клиент-сервер" при удовлетворении запросов от рабочих станций к сегментированной базе данных, находящейся на сервере.
Пусть ? — интенсивность интегрированного потока запросов, поступающего от всех РС, ? — интенсивность потока обслуживания.
Пусть, далее, в силу специфики применения все запросы — простые, т.е. реализуют обращение не более чем к одному сегменту БД каждый и при обслуживании одного запроса не возникает обращений к другим сегментам (что характерно для сложных запросов).
Данную схему функционирования БД можно интерпретировать одноканальной системой массового обслуживания (сервер выполняет функции СУБД) с бесконечной очередью.
Тогда среднее время T*обсл обслуживания одной заявки вычисляется следующим образом:
 |
(2.19) |
где tобсл = 1 / ? — "чистое" время выполнения работ по обслуживанию одной заявки с помощью СУБД, ? - ? / ?.
Разработчики сетевых БД традиционно не учитывают те параметры комплексирования сети, при которых дальнейшая нагрузка на БД (подключение новых РС) становится недопустимой. Ведь T*обсл


Выход из критического положения заключается в использовании не одного, а нескольких серверов, т.е. в переходе к модели многоканальной системы массового обслуживания.
Возможны различные схемы разделения нагрузки между серверами. Это — разделение сегментов БД между серверами при обеспечении связей всех РС с каждым сервером.
Другая схема может предполагать подключение групп РС к одному серверу при возможности использования одним сервером сегментов, расположенных на другом сервере. Такая схема приводит к появлению новых запросов в сети.
Возможна схема, при которой БД дублируется на каждом сервере. Тогда запросы, изменяющие состояние БД, должны "отслеживаться" на каждом сервере.
Все такие схемы затрудняют синхронизацию использования общих данных, усложняют работу СУБД.
Простой выход представляет организация движения, циркуляции сегментов БД между n серверами при подключении каждой РС к одному, "своему" серверу.
Время выполнения заявки при этом увеличивается лишь за счет времени ожидания прихода нужного сегмента на сервер.
Такая схема организации сетевой БД показана на рис. 2.7.

Рис. 2.7. Многосерверная БД с циркулирующими сегментами
Если к каждому серверу подключено примерно одинаковое число k РС, то интегрированный поток запросов делится поровну между серверами, и интенсивность ?серв потока запросов к одному серверу можно считать равной ?/n.
Тогда время обслуживания одного запроса РС вычисляется следующим образом:
 | (2.20) |

Очевидно, что t*обсл = tобсл + tож. Значение tож обусловлено циркуляцией сегментов БД между серверами и без учета "перехвата" другими серверами на пути следования может быть оценено (см. (2.2)):
 | (2.21) |
 | (2.22) |
 | (2.23) |
Здесь n — количество серверов, m — количество сегментов БД, интенсивность запросов пользователя ?польз = ?серв/k, T0 — длительность такта системы.
Тогда очевидно, что рассматриваемая организация сетевой базы данных имеет смысл, если Tобсл << T*обсл.
Отметим, что предлагаемые выше механизмы перемещения информации в сетевой БД, т.е. механизмы активизации ее совокупной памяти, отражают технический уровень построения БД, структуру, способ организации и способ использования памяти ЛВС. Над этим уровнем строится логическая и функциональная сущность БД, которая "не знает", как он устроен. В аналогичной ситуации разработчик программной системы (или транслятор) "не знает" (ибо не опирается на это), как реализуется идея виртуальной памяти компьютера, то есть, каковы механизмы замещения страниц, какова дисциплина замещения и т.д. Это — не его уровень.
В то же время, сегодня мы не можем с уверенностью опровергнуть сомнения в том, что применительно к БД удастся достичь полной независимости таких уровней. Громоздкость выкладок на основе вероятностных оценок, заведомо неполный учет всех факторов говорят, что в целом мы имеем дело с задачей детерминированного имитационного моделирования. Процесс должен быть воспроизведен как можно ближе к реальному, определяя натурный эксперимент. Это позволит оценить действительные возможности сетевого программного обеспечения и технические характеристики ЛВС.
Вместе с тем, здесь не предлагается новый, абсолютный способ организации хранения и использования информации в базах данных, отвергающий все то, что было разработано ранее. Цель настоящей публикации — показать, что существует способ сокращения времени обработки запросов к БД, основанный на организации "встречного" движения информации в ней. Этим способом можно пользоваться частично и весьма обоснованно, для чего предлагаются некоторые соотношения — критерии. Представленные же здесь схемы "рафинированно", по максимуму отражают предложения, но не навязывают каких-либо типовых структур данных.
В этом смысле арсенал средств повышения эффективности базы данных, которым располагает конструктор — разработчик БД, расширяется еще одним средством — средством активизации памяти для "встречного" предложения информации в сетевой базе данных, которым он может воспользоваться после тщательного обоснования. Можно предположить, что различные, прежде всего, по функциональному назначению, БД в разной степени допускают применение предложенного принципа. Например, можно надеяться на то, что встречное движение информации в вычислительной сети способно сократить длину очереди к билетным кассам на поезда дальнего следования.

Принцип работы БД с циркулирующей информацией
Рекомендации по организации вычислений неотделимы от модификации самих методов вычислений, традиционно продолжающих линию минимизации количества операций (привлекательной на уровне счетчиков—вычислителей, работающих с арифмометром или, в лучшем случае, с однопроцессорной ЭВМ 60-х годов). Распараллеливание выдвигает другой критерий эффективности: минимизация длины критического пути в информационно-логическом графе решаемой задачи или максимизация коэффициента загрузки исполнительных устройств системы.
Желание уйти от рекомендаций общего характера приводит к рассмотрению классов задач или отдельных "представительных" задач и к демонстрации их возможностей параллельного решения по SPMD-технологии, привлекающей все большее внимание как разработчиков ВС, так и математиков-программистов. По этой технологии вычислительный процесс организуется так, что единственная программа одновременно запускается на всех исполнительных устройствах — на процессорах ВС, на ЭВМ вычислительного комплекса, на рабочих станциях (РС) ЛВС. В этой программе — монопрограмме — "упрятаны" не только сама конфигурация алгоритма обработки, но и механизмы распределения данных, обрабатываемых по одному и тому же алгоритму, синхронизация исполнителей при обработке общих данных, возможность обработки данных по разным ветвям алгоритма (не путать с векторным способом обработки массивов!), универсальность монопрограммы, инвариантной относительно количества участвующих исполнителей и объемов обрабатываемой информации. При этом важно, что при организации совместных действий исполнительных устройств отсутствуют обращения к операционной системе.
Исследование возможностей применения SPMD-технологии к решению задач обработки баз данных приводит к необходимости превращения ее в систему с многоканальным доступом пользователей - в многоканальную систему массового обслуживания. Программно это выражается в том, что система управления базой данных (СУБД), как монопрограмма, должна быть "размножена" для независимого запуска на каждом исполнительном устройстве, непосредственно связанном с пользователем или участвующем в обработке интегрированного потока запросов пользователей (например, в многопроцессорном сервере).
Однако мы сталкиваемся с рядом трудностей, связанных с существованием "узкого горла", так характерного для обработки БД. Не говоря о технических возможностях носителей информации, во многих случаях допускающих последовательный доступ, следует учесть ряд функциональных особенностей БД, требующих оперативного изменения данных, синхронизации обращения к общим данным или к одним и тем же сегментам БД, а также обработки сложных запросов, динамически формирующих многократное обращение к БД. И все же, как максимально "расширить" это "узкое горло", снизив накладные расходы на доступ к информации и на синхронизацию обращений?
Предлагается способ преобразования централизованной сетевой базы данных из традиционно одноканальной в многоканальную систему массового обслуживания на основе применения SPMD-технологии. Способ заключается в организации встречного движения информации к пользователям, рабочие станции которых располагают копией системы управления базой данных. Целью рассматриваемых построений является минимизация времени обслуживания.
Очевидно, если мы хотим снабдить каждого пользователя своей СУБД, то необходимо обеспечить ему доступ на равных правах с другими пользователями. Это требование касается и БД, в силу своих функциональных особенностей допускающих лишь последовательный доступ. Например, доступ к БД — электронной исторической библиотеке, где информация при обращении не изменяется, является параллельным и независимым. Однако доступ к БД транспортного обслуживания является строго последовательным.
Следовательно, многоканальный доступ может быть реализован лишь тогда, когда организовано последовательное встречное предложение базы данных каждому пользователю. БД должна работать в режиме разделения времени.
Здесь мы реально наталкиваемся на "однобокость" развития методов обработки больших массивов информации. Совершенствуя алгоритмы обработки, мы предполагаем "статичность", "пассивность" системы памяти. Память (совокупная память всей системы) должна стать активной, способствовать процессу хотя бы на основе вероятностных предположений, должна реализовать встречные предложения, способные обеспечить снижение среднего времени выполнения запросов пользователей.
Такой способ активизации памяти, основанный не на покое БД, а на ее движении хотя бы внутри ЛВС, рассмотрим далее.
Мы отдаем предпочтение ЛВС и не исключаем другие применения, так как линии передачи данных, используемые в этих сетях, обладают наибольшим темпом развития, совершенствования, ростом пропускной способности. Именно их современные возможности в первую очередь вселяют надежду на реальность идеи активизации памяти, основанной на оперативном обмене данными.
Традиционно, базы данных, реализованные в ЛВС, делятся на централизованные и распределенные.
В централизованных БД вся информация размещается в памяти сервера. Запрос от каждой рабочей станции поступает на сервер и обрабатывается в порядке общей очереди поступивших заявок от всех РС. СУБД в этом случае является прибором обслуживания в одноканальной системе массового обслуживания с ограниченной или бесконечной очередью. Из практических соображений удобно считать очередь бесконечной.
Распределенная БД, при отсутствии сервера, предполагает разбиение информации на сегменты и их жесткое распределение между рабочими станциями. Такая БД воплощает идею многоканальной системы массового обслуживания, так как СУБД реализована на каждой РС и обслуживает запросы только с данной рабочей станции. Подобное воплощение, на практике обусловленное отсутствием возможностей использования мощного сервера, приводит к уверенности, что реализация многоканального доступа способна не только компенсировать этот недостаток, но и достичь большей пропускной способности БД.
Однако ряд сложностей затрудняет реализацию указанных БД, существенно увеличивая время обслуживания запроса. Эти сложности обусловлены:
необходимостью определения места расположения требуемого сегмента БД;организацией его пересылки в память данной РС (один вариант обслуживания);организацией переадресации запроса к СУБД той рабочей станции, на которой находится требуемый сегмент (другой вариант обслуживания);организацией выдачи результата выполнения запроса на ту РС, где этот запрос был сформирован;синхронизацией множественных обращений к одним и тем же сегментам в случае изменения информации в результате выполнения запросов (например, в системах транспортного обслуживания).
Синхронизация множественных обращений к сегментам БД в случае изменения информации требует применения аналога механизма семафоров с его весьма сложными процедурами, обеспечивающими, например, решение таких типовых задач синхронизации, как задача "взаимного исключения" или "читатели — писатели".
Развитие сетевых технологий и, в частности, рост характеристик средств обмена информацией, на новом уровне выдвигают задачи поиска компромиссных, промежуточных архитектур сетевых БД, воплощающих в себе как идею многоканального доступа, так и синхронизацию производимых изменений информации. Такие БД должны обладать высокой оперативностью, где под этим понимается минимизация среднего времени обслуживания запроса.
Основная идея, предлагаемая в настоящей работе, заключается в активизации совокупной памяти ЛВС, в которой располагается БД. Разбитая на сегменты БД предлагает встречный обмен, встречное предложение своих сегментов рабочим станциям, реализуя различные дисциплины таких предложений. Таким образом, сегменты БД циркулируют среди рабочих станций ЛВС. Такие сетевые БД, в которых производится ротация сегментов, находящихся в памяти каждой РС, назовем ротационными.
В этом случае запрос, сформированный пользователем на рабочей станции, ожидает момента поступления необходимого сегмента в память данной рабочей станции. СУБД данной станции, работая в "традиционном" одноканальном режиме обслуживания, выполняет запрос, вводя, если необходимо, изменения в сегмент. Далее, измененный уже сегмент продолжает маршрут своего перемещения. Развивая этот принцип, следует согласиться с тем, что дисциплина перемещения сегментов должна существенно зависеть от интенсивности обращений к конкретным сегментам. Например, некоторые сегменты, относящиеся к архивным, могут не участвовать в циркуляции. В циркуляции сегментов могут временно не участвовать и некоторые рабочие станции, если интенсивность запросов с этих станций резко снижается. Например, студент затребовал учебное пособие, с которым проработает несколько часов.На это время он вправе отключить себя от системы циркуляции БД, дополнительно загружающей ("тормозящей") компьютер. При необходимости он сможет подключиться вновь.
Сетевые базы данных с циркулирующими запросами-предложениями
Рассматриваемым ниже базам данных соответствует архитектура ЛВС с сервером типа "звезда" (рис. 2.5).

Рис. 2.5. База данных с циркуляцией запросов-предложений
Пусть централизованная БД, расположенная на сервере, содержит список свободных сегментов, которые не обрабатываются в данный момент ни одной РС, а также список занятых сегментов, т.е. обрабатываемых рабочими станциями. Не рассматривая сложные запросы либо предполагая их структурирование, требующее последовательного обращения к разным сегментам, допустим, что одна РС может обрабатывать одновременно лишь один сегмент. Таким образом, количество занятых сегментов совпадает с количеством РС, занятых их обработкой.
Располагая списком свободных сегментов, сервер последовательно и циклически опрашивает свободные, т.е. не обрабатывающие ни один сегмент, РС с запросом- предложением: нужен ли ей очередной сегмент из этого списка? Подготавливая запрос, сервер максимально обеспечивает связь с РС для передачи сегмента в случае его необходимости, т.е. производит маршрутизацию.
Если пользователь сформировал запрос к БД со своей РС, то запрос (а по нему определяется необходимый сегмент БД) ожидает прихода запроса-предложения сервера относительно нужного сегмента. Тогда сервер направляет сегмент (точнее, его копию) на РС и этот сегмент переходит в список занятых.
Рабочая станция, закончившая обработку запроса к БД, возвращает в общем случае измененный сегмент серверу. Сегмент переходит в список свободных и впредь участвует в циклическом предложении свободным РС.
Таким образом, время выполнения каждого запроса к БД зависит от состояния сегмента (свободен — занят), от среднего времени обработки сегмента используемой СУБД, от времени одного цикла циркуляции запросов-предложений, от организации и подготовки обмена информацией (маршрутизации) в сети и т.д.
Отметим важность средств обеспечения надежности, защиты данных, отображения и др.
Рассчитаем среднее время обслуживания запроса при рассматриваемой организации его обработки.
Пусть, как и прежде, m — количество сегментов БД, n — количество РС в ЛВС. Для поиска вероятности того, свободен ли требуемый сегмент или взят на обработку (занят), необходимо определить в стационарном режиме среднее число занятых сегментов БД.
Считая поток запросов простейшим, построим цепь Маркова (рис. 2.6), соответствующую многоканальной системе массового обслуживания с количеством n каналов [17].

Рис. 2.6. Цепь Маркова для нахождения предельных вероятностей состояния сегментов БД
Состояние S0 соответствует отсутствию занятых сегментов, поток запросов при этом реализуется полностью, т.е. ?0 = n ?польз. На обратный переход в это состояние влияет поток обслуживания с интенсивностью ?, формируемый копией СУБД единственной РС. Состояние S1 соответствует наличию одного занятого сегмента. Так как одна РС оказывается занятой обработкой сегмента, то поток запросов к БД реализуется n - 1 свободными. Кроме того, из этого потока исключаются запросы к занятому сегменту. Тогда

Таким образом, для состояния Si, i = 0 , ..., n, когда занято i сегментов,
 | (2.11) |
Уравнения Колмогорова имеют вид
 | (2.12) |
 | (2.13) |
 | (2.14) |
 | (2.15) |
tожид своб. = 0,5 (m - q) tпредл. (2.16)
Если сегмент, к которому произведен запрос, занят, то время tожид. зан. его ожидания зависит от времени окончания его обработки, от времени tвозвр возврата серверу, от времени tосвоб включения в число свободных и от времени его ожидания как свободного сегмента:
tожид.зан. = 0,5 tобсл. + tвозвр. + tосвоб. + tожид своб. (2.17)
Тогда полное время обслуживания запроса с РС вычисляется:
Tобсл = Pзанят tожид.зан + (1 - Pзанят)tожид своб + tобсл. (2.18)
Полученная оценка, аналогично (2.5) и (2.10), является основой критерия эффективности данного способа организации сетевой БД.
Анализ сетевых топологий и обоснование
В связи с распространением персональных компьютеров и созданием на их основе автоматизированных рабочих мест (АРМ) возросло значение локальных вычислительных сетей (ЛВС). Правильно организованная и умело эксплуатируемая сеть обеспечивает целый ряд преимуществ по сравнению с отдельным компьютером.
Распределение данных (Data Sharing). Данные в сети хранятся на центральном РС и могут быть доступны для любого РС, подключенного к сети, поэтому не надо на каждом рабочем месте хранить одну и ту же информацию.Распределение ресурсов (Resource Sharing). Периферийные устройства могут быть доступны для всех пользователей сети, например: принтер, факс-модем, сканер, диски, выход в глобальную сеть.Распределение программ (Software Sharing). Все пользователи сети могут иметь доступ к программам, которые были один раз централизованно установлены.Электронная почта (Electronic Mail). Все пользователи сети могут передавать и принимать сообщения.Обеспечение широкого диапазона решаемых задач, предъявляющих повышенные требования к производительности и объему памяти.
Локальные сети имеют некоторые особенности.
Главная из них — это связь. Она должна быть быстрой, надежной и удобной. Обычно, локальные сети не выходят за пределы нескольких комнат или одного здания, поэтому длина линии связи обычно не превышает нескольких сотен метров. Они связывают между собой ограниченное количество РС. Все это позволяет обеспечить качественную связь. Поэтому скорость передачи данных обычно составляет от 10 Мбит/с и выше. К тому же, требуется надежная связь, иначе при исправлении ошибок теряется выигрыш в скорости. Также необходимо небольшое время ожидания установления связи, так как оно включено в общее время передачи информации. При таких высоких требованиях в локальных сетях используются специальные технические средства.
При построении сетей ЭВМ, в т.ч. локальных, говорят о их топологии.
Топология — описание способа, при помощи которого рабочие станции и серверы физически соединяются между собой. Топологии различаются требуемой длиной соединительного кабеля, удобством соединения, возможностями подключения дополнительных абонентов, отказоустойчивостью, возможностями управления обменом. Топологическая структура влияет на пропускную способность и стоимость локальной сети. Каждая топология сети налагает ряд условий. Например, она может диктовать не только тип кабеля, но и способ его прокладки. Отличительной особенностью ЛВС является наличие моноканала, т.е. единственного маршрута, связывающего любые две станции. В связи с этим при подключении устройств к сети используются три топологии.
Кольцевая сеть FDDI, IBM Token Ring)
"Кольцо" — последовательное соединение абонентов в замкнутое кольцо (рис. 3.2), что и определяет его особенности. Во-первых, вся передаваемая информация проходит через всех абонентов. Поэтому выход из строя любого из них нарушает работу всей сети в целом. Во-вторых, разрыв кабеля в любой точке нарушает целостность кольца и выводит из строя всю сеть. Для этого применяют дублирование кабеля. Управление может быть как централизованным, так и децентрализованным, оно не так жестко зависит от топологии, как в случае "звезды". Все адаптеры должны быть одинаковы, но иногда один из них выполняет функции диспетчера сети, тогда он значительно сложнее.

Рис. 3.2. "Кольцевая" сеть
Эта топология допускает большое число абонентов, причем возможно изменение их количества. В кольце происходит автоматическое усиление передаваемого сигнала каждым абонентом, поэтому его размеры могут быть очень большими, и ограничены они только временем прохождения сигнала по всему кольцу.
Концепция построения вычислительных комплексов на базе локальной вычислительной сети
Технический прогресс, несомненно, сказывается на увеличении частоты работы элементной базы, на повышении степени интеграции, но технический же прогресс приводит к появлению все новых задач, требующих еще более значительного роста производительности вычислительных средств. Это можно считать законом, приводящим к новым уловкам при совмещении работы устройств ВС, при увеличении их количества в системе, при увеличении их эффективности в процессе решения задач.
Под эффективностью работы устройства в составе ВС или компьютера в составе ВК понимают степень его участия в общей работе ВС или ВК при решении конкретной задачи — коэффициент загрузки устройства (компьютера). Распараллеливание работ оправдано, если приводит к существенному росту усредненного по всем устройствам (компьютерам) коэффициента загрузки оборудования при решении задач. Это непосредственно сказывается на времени решения. Сегодня говорят не о специальном классе задач, а о задачах, ориентирующих ВС и ВК на универсальность, что обусловлено современными областями применения.
Важным революционизирующим моментом стал переход на микропроцессорную элементную базу, обусловившую построение мультимикропроцессорных ВС для параллельной обработки информации или компьютерных сетей для распределенной обработки информации.
Основная сложность распараллеливания заключается в соблюдении частичной упорядоченности распределяемых работ. Поэтому решение задач синхронизации параллельного вычислительного процесса в ВС или распределенного вычислительного процесса в ВК сопровождает все усилия по организации совместной работы устройств. Организация распределенного вычислительного процесса предъявляет повышенные требования к скорости синхронизирующего взаимного обмена данными, что и послужило сдерживающим фактором применения ВК.
Необходимость оперативного решения сложных задач стимулирует усилия по разработке дорогих и уникальных супер-ЭВМ. Однако на новом витке развития все более привлекательной становится идея возврата к использованию коллектива компьютеров, совместно решающих общую задачу, — идея построения ВК для распределенной обработки информации.
Эта идея связана с развитием сетевых технологий, достигших такого уровня, когда оперативность взаимодействия компьютеров в сети позволяет расширить применение сетей. Построение ВК на основе компьютерной сети (в пространстве компьютерной сети) должно привлечь своей естественностью, достаточностью аппаратных и программных средств, не требующих дополнительных разработок, непреложным развитием сетей вне зависимости от данного применения.
Сетью ЭВМ называется комплекс территориально рассредоточенных ЭВМ и терминальных устройств, связанных каналами передачи данных.
Сейчас сложилась такая практика, что с сетями ЭВМ связывают более общее понятие — информационная система. Однако изначально целью создания сетей ЭВМ было:
Совместное использование суммарных вычислительных ресурсов. (Данная цель характерна на ранней стадии распространения сетей. Когда-то восторг вызывало то, что задача, введенная в Нью-Йорке, в действительности решалась в Париже — в соответствии с наличием вычислительных ресурсов.)
Обеспечение широкого диапазона решаемых задач, предъявляющих повышенные требования к производительности и объему памяти. (На возможность распараллеливания возлагались также надежды на этапе разработки первых сетей ЭВМ. Однако возврат к этой идее наблюдается сейчас: в распределенных вычислительных комплексах, используемых в системах управления, в том числе — бортовых, все настойчивее изыскиваются возможности применения сетевых технологий, весьма продвинутых в направлении стандартизованного оперативного обмена.)
Обеспечение высокой надежности систем обработки информации (за счет возможности перераспределения выделяемых ресурсов).
Совместное и взаимное информационное обслуживание, расширение сети пользователей ЭВМ, развитие качественно новых средств коммуникаций. (Обмен данными и совместное использование централизованных или распределенных банков данных.)Социальный прогресс, обусловленный культурным, научным, деловым обменом, общедоступностью информации наряду с возможностями адресной передачи. (Качественно новый уровень достигнут в культурном обмене, в дистанционном обучении, в проведении научных конференций, в демонстрационном показе и рекламе, в деловых контактах, в оперативности передачи значительных объемов данных по Еmail электронной почте и т.д.)
Таким образом, все большую актуальность обретает задача расширения возможностей сетей ЭВМ за счет возложения на них функций распределенных вычислительных комплексов для решения задач высокой сложности. На первом этапе речь может идти о локальных сетях (ЛВС), обладающих наиболее оперативным обменом. По-видимому, рано говорить о массовом применении сетей для решения задач управления в реальном масштабе времени, здесь требуемая оперативность обмена может быть не достигнута на уровне современных сетевых технологий. Однако в рамках современных представлений о сложности алгоритмов (например, о NP-сложных задачах) накладные расходы на обмен информацией в сети могут быть ничтожны по сравнению с общим временем решения задачи, обусловленным, в частности, применением методов перебора.
Чтобы избежать здесь голословных лозунгов, необходимо создавать и накапливать опыт решения сложных задач в компьютерных сетях. Такой подход позволит выявить и сформировать технологию подготовки и программирования подобных задач, поможет сформулировать требования к развитию аппаратных, программных и языковых средств, покажет область эффективного применения сетевых технологий решения задач.
Сказанное выше тем более важно сейчас, когда умы охватывает идея Grid-технологий — технологий предоставления сетью (включая Интернет) виртуальных ресурсов по запросам на решение сложных вычислительных задач.
Локальная сеть Ethernet
В настоящее время разными фирмами разработаны стандарты ЛВС, поддержанные аппаратно и программно. Наиболее распространенным стандартом, соответствующим требованиям режима вычислительного комплекса, является локальная сеть ETHERNET. (Спецификацию разработали компании Xerox Corporation, Digital Equipment Cjrporation (DEC), Intel Corporation.)
На базе Ethernet разработан стандарт IEEE 802.3. Сеть предполагает несколько конфигураций. Использует коаксиальный или оптоволоконный кабель.
Применяется топология "шина", т.е.:
все устройства, подключенные к сети, равноправны, т.е. любая станция может начать передачу в любой момент времени, если передающая среда свободна;данные, передаваемые одной станцией, доступны всем станциям сети.
Для организации взаимодействия станций в сети используется метод Множественного Доступа с Контролем Несущей и Обнаружением Столкновений (МДКН/ОС) — Carrier Sense Multiple Access / Collision Detection (CSMA/CD).
Контроль Несущей: во время работы станция постоянно проверяет среду передачи. Передающая среда может быть
свободна, т.е. ни одна другая станция не передает данные;занята, т.е. идет передача данных другой станцией.
Множественный Доступ: при использовании метода любая станция, обнаружив, что среда свободна, может начать передачу своих данных. Поэтому возможна ситуация, когда одновременно несколько станций начнут передавать данные.
Обнаружение Столкновений (Коллизий): станция, обнаружившая коллизию, выдает другим станциям специальный сигнал, по которому переданная информация считается недостоверной. После этого каждая станция делает повторную попытку передачи через специально найденное ею случайное время. Разное для всех станций случайное смещение времени повторной передачи служит высокой вероятности избежания коллизии. (Оригинальный способ избежать централизованного управления!) Если за 16 попыток станция не смогла передать пакет, считается, что среда неисправна. В локальную сеть всегда входит несколько абонентов, и каждый из них в любой момент времени может обратиться к сети. Поэтому требуется управление обменом с целью упорядочения использования сети различными абонентами, предотвращение или разрешение конфликтов между ними. В противном случае возможно искажение передаваемой информации. Для управления обменом (или управлением доступом к сети, или арбитража сети) используются различные методы, особенности которых определяются выбранной топологией сети.
Организация параллельного решения задачи в локальной сети
Распараллеливание метода "сеток" с очевидностью адекватно второму способу распараллеливания, что и должно определить направление поиска. То есть можно с уверенностью заявить, что распределение узлов сетки между процессорами ВС (распараллеливание по информации), ЭВМ вычислительного комплекса или рабочих станций сети является эффективным способом параллельного решения системы дифференциальных уравнений в конечных разностях.
В лекции 1 рассматривался пример решения уравнения в частных производных. Далее на этом примере будут показаны схемы возможной реализации метода сеток в ЛВС.
По рис. 1.12 из курса "Архитектура параллельных вычислительных систем" мы можем полностью представить различные планы параллельного решения рассмотренной задачи.
Метод матричных вычислений характерен для матричных вычислительных систем. В таких системах организуются "быстрые" связи между процессорами в соответствии с преимущественными направлениями обменов информацией. Обычно это связи по строке и по столбцу с соединением "последнего с первым". Матрица процессоров "накладывается" на множество узлов сетки, воспроизводящее такую же матрицу, и узлы обрабатываются. Матрица процессоров циклически обходит матрицы узлов сетки.
Другая стратегия распределения узлов между процессорами может быть основана на делении области задания функции между процессорами. Т.е. вся область D на рис. 1.12 из курса "Архитектура параллельных вычислительных систем" может быть разделена поровну между процессорами ВС или станциями сети.
Третья стратегия может предусматривать нумерацию процессоров, превращение многомерного (в примере — двумерного) массива узлов сетки в одномерный линейный и назначение каждого узла на процессор с номером, равным остатку от деления его номера на число используемых процессоров. Эта стратегия, в наибольшей степени обеспечивающая инвариантность программы счета относительно числа узлов и числа используемых процессоров, соответствует рассмотренной ранее SPMD-технологии.
Равноправие процессоров (симметричность) делают целесообразным использование шинной архитектуры ЛВС. (Отметим, что на ранней стадии построения вычислительных комплексов применялась именно шинная архитектура, как наиболее простая и естественная. То же можно отметить и относительно многих современных и перспективных мультимикропроцессорных систем.) Распространенным стандартом такой архитектуры, обусловившим разработку широкой номенклатуры аппаратных средств, является сеть ETHERNET. Параллельный вычислительный процесс должен воспроизводить технологию SPMD, основанную на применении способа распараллеливания по информации.
Тогда организация параллельной обработки информации и схема вычислений должна быть следующей.
Исследуется задача и выделяется основной массив данных (одномерный или многомерный), обработку которого целесообразно распределить между станциями ЛВС, — опорный массив.Формируется план распределения элементов опорного массива для обработки станциями сети. Разнообразие таких планов порождает и разнообразие возможных способов переадресации. Например, весь опорный массив может быть поровну (со следующими подряд элементами) поделен между станциями. Такой способ может применяться в случае, если длина массива не изменяется динамически. Более универсален способ распределения элементов опорного массива, когда после "расчета по n" каждый из них оказывается закрепленным за станцией с тем же номером. Это в точности соответствует технологии SPMD и поддержано системой команд. Такое распределение допускает динамическое изменение длин массивов (поддерживает динамический тип данных), что крайне важно при обработке баз знаний.Составляется единственная для всех станций (предполагается их программная совместимость), универсальная программа циклической обработки элементов опорного массива, закрепленных за одной станцией. Программа должна содержать критический интервал обмена данными между станциями в необходимых (по алгоритму) направлениях. При этом запрос с последующим ожиданием данных (принцип редукционных вычислительных систем) должен отсутствовать, данные должны только отправляться. Это значит, что программы должны "уметь" ждать необходимые для себя данные. Поэтому становится целесообразным воспроизведение принципа data flow с помощью "почтовых ящиков".Составляется программа ввода, визуализации и управления вычислительным процессом для станции (персонального компьютера), который назначается мониторным.Задача решается в диалоговом режиме. Дело в том, что при большом времени собственно решения вмешательство пользователя (оператора) может быть не только неизбежным, но и желательным. Например, нахождение всех экстремумов функции можно автоматизировать следующим образом: разделить область задания функции между компьютерами и поручить им полностью исследовать свои подобласти; затем заставить их совместно исследовать полученные результаты и выделить глобальные экстремумы и др. Вторая задача может оказаться существенно сложнее. В то же время оператором она может быть решена значительно проще при достаточной визуализации. Принятое им решение может быть немедленно использовано при последующем автоматическом решении этой или другой задачи.
Рассмотрим конкретный возможный план решения рассмотренной выше задачи методом "сеток". Для простоты положим число используемых процессоров равным 2. В основу плана положим способ разделения области D между процессорами поровну. Зафиксируем hx = hy = h, определив тем самым количество узлов сетки в каждой строке и в каждом столбце. На рисунке 3.6 отражены выбранные количества узлов в строках и столбцах. Первая и последняя строка, как и первый и последний столбец, соответствуют узлам, в которых заданы граничные значения функции-решения.

Рис. 3.6. Распределение данных между двумя процессорами для решения задачи методом "сеток"
Область D1, обрабатываемая процессором 1, определяется границами индекса i и координаты x:

Область D2, обрабатываемая процессором 2, определяется границами индекса i и координаты x:

По второй координате 0


На рисунке показана передача промежуточных значений узлов процессором процессору для счета узлов, использующих эти значения. Такая передача может осуществляться либо непосредственно после нахождения очередного приближения значения функции в узле, либо после очередной итерации — для всех необходимых значений сразу. Второй способ может значительно сократить время выполнения обмена, хотя задерживает использование узлов.
Важен выбор способа нахождения начального значения функции — решения в узлах. Этот выбор влияет на скорость сходимости решения.
В соответствии с граничными условиями
fi0 = f1(ih,0) i = 0, ..., n - 1,
fi,m-1 = f2(ih,(m-1)h=B) i = 0, ..., n - 1,
f0j = f3(0,jh) j = 0, ..., m - 1,
fn-1,j = f4((n-1)h=A,j) j = 0, ..., m - 1.
Нулевое приближение значений fij может быть рассчитано по формулам интерполяции с усреднением:

для всех 0 < i < A, 0 < j < B.
Итерационная формула имеет общий вид fij = F(fi-1,j, fi+1,j, fi,j-1, fi,j+1).

Шинная организация (Ethernet, ARCnet)
"Шина" — ориентирована на полное равноправие всех абонентов и идентичность их адаптеров (рис. 3.3). Это не означает, что управление обменом не может быть централизованным. Однако центр будет заниматься только управлением обменом, а не перераспределением информации. "Шина" может логически работать как "звезда" или "кольцо". "Шина", в отличие от других топологий, сильно зависит от электрического согласования используемых линий связи, потому что при любом повреждении кабеля возникают отражения и наложения сигналов. В таком случае нарушается работа всей сети. Однако, к выходу из строя компьютеров данная топология не чувствительна, нарушается обмен только с поврежденным компьютером, а вся остальная сеть остается в рабочем состоянии. Максимально допустимое количество абонентов в "шине" такое же, как и в "кольце". В "шине" легко менять количество подключенных абонентов, иногда даже в процессе работы. В связи со сложностью децентрализованного обмена, сложность аппаратуры в адаптерах выше, чем в других топологиях. Однако децентрализованное управление гораздо надежнее централизованного и лучше приспосабливается к изменяющимся внешним условиям.

Рис. 3.3. Сеть с общей шиной
Существуют также смешанные топологии, такие как "звезда-шина", "звезда-кольцо", которые имеют свои преимущества.
Таблица 3.2. Сравнение топологий сетей
ПараметрыЗвездаКольцоШина1. Отказоустойчивость2. Количество абонентов3. Изменение количества абонентов4. Влияние на общую стоимость сети5. Возможность управления обменом6. Особенности7. Протяженность8. Применение| Выход из строя одного PC не влияет на работоспособность сети | Выход из строя одного PC может вывести из строя всю сеть | Выход из строя кабеля останавливает работу многих пользователей |
| 16 | 1024 и выше | 1024 и выше |
| Возможно | Требует остановки всей сети | Легко изменяется |
| Дополнительные затраты на центральный компьютер | Дополнительные затраты на адаптер, выполняющий функции диспетчера сети | Дешевая среда передачи |
| Централизованное | Централизованное и децентрализованное | Децентрализованное |
| Мощность всей сети зависит от сервера | Количество пользователей не оказывает сильного влияния на производительность. Трудно локализовать проблемы | Оптоволоконные кабели не применяются. При значительных объёмах трафика уменьшается пропускная способность. Трудно локализовать проблемы. |
| До нескольких десятков километров | ||
| В зависимости от предъявляемых требований | ||
Для организации распределенных вычислений необходимо выбрать такую топологию сети, которая поддерживает равноправную, "симметричную" связь "каждый с каждым". Среди рассмотренных топологий таким требованиям в максимальной степени соответствует шинная архитектура. Преимущества этой архитектуры отображены исторически при практическом объединении ЭВМ в распределенные вычислительные комплексы для совместного решения сложных задач.
Сложность алгоритма и проблема распараллеливания
Ранее уже использовалось понятие сложности. Рассмотрим его полнее.
Пусть задан некоторый алгоритм A. Почти всегда существует параметр n, характеризующий объем его данных. Пусть функция T(n) — время выполнения A, а f — некоторая функция от n. Говорят, что алгоритм A имеет теоретическую (асимптотическую) сложность O(f(n)), если

где k — действительное.
Если алгоритм выполняется за фиксированное время, не зависящее от размера задачи, говорят, что его сложность равна O(1).
Это определение обобщается в случае, если время выполнения существенно зависит от нескольких параметров. Например, алгоритм, определяющий, входит ли множество m элементов в множество n элементов, может иметь, в зависимости от используемых структур данных, сложность O (m n) или O (m+n).
Практически время выполнения алгоритма может зависеть от значений данных. Так, время выполнения некоторых алгоритмов сортировки существенно сокращается, если первоначально эти данные были частично упорядочены. Чтобы учитывать это, сохраняя возможность анализировать алгоритм независимо от их данных, различают:
максимальную сложность, определяемую значением Tmax(n) — время выполнения алгоритма, когда выбранный набор n данных порождает наиболее долгое время выполнения алгоритма;среднюю сложность, определяемую значением Tср(n) — средним временем выполнения алгоритма, примененного к n произвольным данным.
Эти понятия без труда распространяются на измерение сложности в единицах объема памяти: можно говорить о средней и максимальной пространственной сложности.
Самыми лучшими являются линейные алгоритмы, имеющие сложность порядка an=b. Они называются также алгоритмами порядка O(n) где n — размерность входных данных. Такие алгоритмы действительно существуют. Например, сложение двух чисел столбиком в случае, если одно из них состоит из n, а другое — из m цифр, требует не более max(n, m) сложений и не более max(n, m) запоминаний. Т.е. данный алгоритм имеет сложность порядка O(n+m). Разумеется, это выражение показывает только порядок величины — постоянные факторы в нем не учитываются.
Обобщение линейности дает нам первый большой класс алгоритмов — полиномиальных.
Полиномиальным (или алгоритмом полиномиальной временной сложности) называется алгоритм, у которого временная сложность есть O(p(n)), где p(n) — полином от n. Задачи, где для решения известен алгоритм, сложность которого составляет полином заданной, постоянной и не зависящей от размерности входной величины n степени, называют "хорошими" и относят их к классу P.
Экспоненциальной по природе считается задача сложностью не менее порядка xn, где x — константа или полином от n. Например, это задачи, в которых возможное число ответов уже экспоненциально. В частности, к ним относятся задачи, где требуется построить все подмножества заданного множества или все поддеревья заданного графа. Экспоненциальные задачи относят к классу E.
Соответственно, и алгоритмы, в оценку сложности которых n входит в показатель степени, относятся к экспоненциальным.
Необходимо отметить, что при небольших значениях n экспоненциальный алгоритм может быть даже менее сложным, чем полиномиальный. Тем не менее, различие между этими типами алгоритмов весьма велико и проявляется при больших значениях n.
Особую группу по значениям сложности, близким к полиномиальным, составляют алгоритмы, сложность которых является полиномиальной функцией от log n (поскольку log n растет медленнее, чем n).
Для большей убедительности и сравнения полиномиальных и экспоненциальных алгоритмов приведем таблицу, где единица времени — 1 мкс, а сложность совпадает с необходимым количеством единиц времени для обработки набора n данных:
Таблица 3.1. Сложность и время выполненияСложностьРазмер задачи — n102030405060nn?n?n52n3n
| 0.00001 с | 0.00002 с | 0.00003 с | 0.00004 с | 0.00005 с | 0.00006 с |
| 0.0001 с | 0.0004 с | 0.0009 с | 0.0016 с | 0.0025 с | 0.0036 с |
| 0.001 с | 0.008 с | 0.027 с | 0.064 с | 0.125 с | 0.216 с |
| 0.1 с | 3.2 с | 24.3 с | 1.7 мин | 5.2 мин | 13.0 мин |
| 0.01 с | 1.0 с | 17.9 мин | 12.7 дней | 35.7 лет | 366 веков |
| 0.59 с | 58 мин | 6.5 лет | 3855 веков | 2·108 веков | 1.3·1013 веков |
Приведенная таблица иллюстрирует причины, по которым полиномиальные алгоритмы считаются более предпочтительными, чем экспоненциальные.
Уточним понятие сложности для итеративных и рекурсивных алгоритмов.
Отнесем к итеративным алгоритмам и те, к которым сводятся рекурсивные алгоритмы (например, вычисление факториала n!). Тогда время их выполнения (в случае сходящегося процесса) зависит от главного условия повторения итерации, например, от требуемой точности. Если мы установим время или сложность одной итерации, то сможем умножением на число итераций установить максимальную или среднюю сложность. Число итераций устанавливается теоретически или экспериментально. Например, так можно сделать при расчете значений функций по их разложению в ряд.
Однако иногда приходится решать оптимизационную задачу, выбирая между сложностью одной итерации и количеством итераций.
Для большинства конечно-разностных схем решения дифференциальных уравнений методом сеток можно считать, что сложность одной итерации составляет O(n2) или O(n ? m), где n2 — количество узлов при равном разбиении по x и по y, а n? m — то же количество при различающемся разбиении по осям. Увеличение количества узлов, покрывающих ту же область, т.е. уменьшение hx и hy, увеличивает скорость сходимости - и, соответственно, уменьшает число итераций, но сложность каждой итерации растет квадратично. Значит, необходим компромисс, который достигается посредством изучения поведения процесса, как на теоретическом, так и на экспериментальном уровне, вплоть до автоматической коррекции шагов в процессе вычислений в зависимости от локального поведения аппроксимаций производных. Т.е. шаги становятся непостоянными во всей области.
Однако по своей природе действительно рекурсивные алгоритмы по сложности относятся к классу экспоненциальных алгоритмов. Как правило, это задачи оптимизации, основанные на переборе (алгоритмы с возвратом, метод "ветвей и границ").
Имеется широко распространенное соглашение, по которому задача не считается "хорошо решаемой", пока для нее не получен полиномиальный алгоритм.
Задача называется труднорешаемой, если для ее решения не существует полиномиального алгоритма.
Эта градация относительна, ибо сложность определяется по наихудшему варианту. Хотя реализация метода "ветвей и границ" — труднорешаемая задача (при теоретической оценке по максимальной сложности), сейчас для многих задач известны такие алгоритмы, которые практически очень быстро находят решение именно методом ветвей и границ.
Однако есть понятие гарантированных и негарантированных оценок. Если сложность задачи полиномиальная, мы можем уверенно предсказать оценку времени решения. При решении задачи методом "ветвей и границ" незначительное изменение начальных данных даже без изменения размерности задачи может непредсказуемо привести к резкому скачку в увеличении времени решения. Т.е. существует большой разрыв между значениями теоретической максимальной сложности и практической средней сложности экспоненциальных алгоритмов. Постоянно ведутся поиски более эффективных экспоненциальных алгоритмов.
Полиномиальные по сложности алгоритмы относят к классу P-сложных. Среди экспоненциальных выделяют алгоритмы, основанные на переборе, и их относят в класс NP-сложных. Т.е. формально возможно существование экспоненциальных алгоритмов, основанных не на переборе. Например, n!, растущий быстрее, чем 2n. К NP-сложным относятся, например, задачи линейного целочисленного программирования, составление расписания, поиск кратчайшего пути в лабиринте и т.д. Обратим внимание, что все это так называемые дискретные задачи — на основе "неделимых" объектов.
В данном контексте мы и будем понимать термин "задача высокой сложности", представляя важность применения методов распараллеливания.
Управление обменом в сети типа "шина"
В этой топологии (рис. 3.4) возможно такое же централизованное управление, как и в "звезде" (т.е. физически сеть — "шина", но логически — "звезда"). При этом один из абонентов ("центральный") посылает всем остальным ("периферийным") запросы, выясняя, кто хочет передать, и затем разрешает передать одному из них. После окончания передачи абонент сообщает "центру", что он закончил, и "центр" снова начинает опрос. Все преимущества и недостатки такого управления - те же, что и в случае "звезды". Единственное отличие в том, что центр не перекачивает информацию от одного абонента другому, а только управляет доступом.

Рис. 3.4. Сеть с общей шиной — логическая "звезда"
Однако чаще в "шине" реализуется децентрализованное управление, так как аппаратные средства абонентов одинаковые. При этом все абоненты также имеют равный доступ к сети, и решение, когда можно передавать, принимается каждым абонентом на месте, исходя из анализа состояния сети. Возникает конкуренция между абонентами за захват сети, и, следовательно, возможны конфликты между ними и искажения передаваемых данных из-за наложения пакетов.
Существует множество алгоритмов (сценариев) доступа, часто очень сложных. Их выбор зависит от скорости передачи в сети, от длины шины, загруженности сети (интенсивности обмена или трафика сети). Иногда для управления доступом к шине используется дополнительная линия связи. Это упрощает аппаратуру контроллеров и методы доступа, но заметно увеличивает стоимость сети в целом за счет удвоения длины кабеля и количества приемопередатчиков. Поэтому данное решение не получило широкого распространения.
Можно отметить ряд существующих методов обмена в сетях шинной архитектуры.
Простейший метод, используемый при выбранном коде обмена NRZ в сравнительно медленных сетях, — децентрализованный кодовый приоритетный арбитраж. Данный метод арбитража был предложен Институтом Проблем Управления (ИПУ) еще в начале 1970-х годов.
Он характеризуется низкой скоростью передачи, но высокой надежностью. Все абоненты имеют собственные приоритеты, которые могут динамически изменяться в зависимости от важности информации. При малой интенсивности обмена все абоненты равноправны (вероятность столкновений очень мала). Величина времени доступа к сети здесь не может быть гарантирована, так как абоненты с высокими приоритетами могут надолго занять сеть, не позволяя начать передачу абонентам с низкими приоритетами.
Второй метод, используемый в шине, — децентрализованный временной приоритетный арбитраж или метод доступа (рис. 3.5). Этот метод управления обменом обеспечивает более высокую скорость обмена, чем предыдущий (поскольку здесь нет ограничения на длительность каждого бита). Практически реализовать его так же сложно, как и предыдущий (каждый абонент должен отсчитывать свой временной интервал). Недостаток метода состоит также в том, что в случае большой длины сети и большого количества абонентов задержки становятся очень большими. Пример: при длине сети 1км, задержке сигнала в кабеле 4 нс/м и количестве абонентов 256 двойное время прохождения сигнала в сети 2L/V (L — полная длина сети, V — скорость распространения сигнала в используемом кабеле), или минимальная задержка составит 8 мкс. Следовательно, для абонента с сетевым адресом 255 задержка будет уже равна 255*8мкс=2040 мкс, т.е. около 2 мс, что уже довольно существенно. Для сравнения: если пакет имеет размер 1 Кбайт, то при скорости передачи 10 Мбит/с его длительность будет всего 0,8 мс. Данный метод не имеет жесткой привязки к коду передачи информации (в предыдущем методе можно было использовать NRZ). Код может быть практически любым, главное — выбрать его таким, чтобы можно было определять занятость сети.
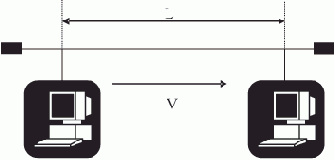
Рис. 3.5. Обмен методом доступа
Третий метод, получивший довольно широкое распространение, можно считать развитием второго. Называется он CSMA/CD (Carrier-Sense Multiple Access/Collision Detection) или по-русски МДКН/ОК — метод доступа с контролем несущей и обнаружением коллизий (столкновений).
Идея метода состоит в том, чтобы уравнять в правах всех абонентов в любой возможной ситуации, то есть добиться, чтобы не было больших и малых фиксированных приоритетов (как в случае второго метода). Для этого используются времена задержки, вычисляемые каждым абонентом по определенному алгоритму.
К достоинствам метода CSMA/CD можно отнести полное равноправие всех абонентов, то есть ни один из них не может надолго захватить сеть. Метод достаточно надежен: ведь в течение всего времени передачи пакета идет контроль столкновений. К недостаткам метода относится то, что он не исключает повторения столкновений, а также плохо держит высокую нагрузку в сети. Обычно считается, что он хорош только до тех пор, пока нагрузка не превышает 30 \%, то есть только 30 \% времени сеть занята, а 70\% времени — свободна. Для сети Ethernet в среднем считается предельно допустимым 50\ldots100 абонентов, иначе возможны существенные нарушения обмена. Основной недостаток метода — негарантированное время доступа: нельзя сказать наверняка, через сколько времени пакет точно дойдет до приемника. В этом отношении он хуже, чем методы централизованного управления (методы опроса).
Звездообразная сеть IBM Token Ring, ARCnet)
"Звезда" — принципиально централизованная топология (рис. 3.1), в которой всегда есть четко выделенный центральный абонент, осуществляющий все управление обменом в сети, и через который идет вся информация в сети. В этом есть свои плюсы и минусы. Любое жестко централизованное управление по своей сути бесконфликтно, но такая сеть не будет работать при любой неисправности центрального абонента. Поэтому центральный компьютер должен отличаться от остальных высокой надежностью, а, следовательно, и более высокой стоимостью. К тому же, выполнять другие задачи на центральном компьютере станет невозможно, так как он будет загружен работой с сетью. К недостаткам топологии относится также ограниченное число абонентов, которое обычно в локальных сетях не превышает 16 пользователей. Затруднительно соединение звезд между собой. К плюсам данной конфигурации можно отнести ее малую чувствительность к выходу из строя соединительного кабеля. Разрыв кабеля в любом месте всегда нарушает связь только с одним абонентом.

Рис. 3.1. Сеть типа "звезда"
Графический метод решения и его обобщение
Рассмотрим пример
z=c1x1+c2x2=2x1+5x2

при ограничениях
q1=x1

q2=x2

q3=x1+x2

и условиях x1


Каждое ограничение в двухмерном пространстве, n=2, определяет полуплоскость. Их пересечение образует многоугольник R (рис. 4.1). Его грани — прямые, получены на основе ограничений, в которых неравенства заменены равенствами.
q1 = 40
q2 = 30 (4.2)
q3 = 50
Эти равенства образуют уравнения границ или просто границы R.

Рис. 4.1. Графический метод решения задачи линейного программирования
Этот многоугольник (выпуклый многогранник; выпуклый, — ибо он остается по одну сторону от любой прямой, проходящей через его ребро) представляет собой допустимое множество решений R задачи ЛП.
Выберем произвольное значение, например, z=100 целевой функции. Прямая 2x1+5x2=100 показана на рисунке. Она пересекает ось x1 в точке x1=50 и ось x2 в точке x2=20.
Отметим, что для

Т.к. dx1 и dx2 принадлежат прямой z, то скалярное произведение двух векторов, которое здесь изображено, равно нулю в том случае, если вектор (c1, c2) =(2, 5) перпендикулярен прямой z.
Увеличиваем значение z, передвигая (с помощью линейки) прямую — целевую — функцию параллельно самой себе в сторону ее возрастания вдоль вектора (2, 5) до тех пор, пока линейка не коснется последней возможной точки многогранника. R. Это значение z и будет максимальным. В данном случае — это точка A = (x1=20, x2=30).
Сделаем важное замечание относительно многогранника R.
То, что он выпуклый, мы заметили ранее.
Нам были заданы три ограничения, отсекающие полуплоскости, но определившие не все границы многогранника R. С "не закрытой" ими стороны область R оказалась закрытой условиями неотрицательного решения задачи: x1


При этом не все условия могут быть переведены в ограничения. В нашей задаче могло существовать некоторое ограничение q4 (на рисунке пунктиром), которое бы определяло границу R слева, исключая границу x1 = 0.
При этом граница x2 = 0 внизу осталась бы.
Другое важное замечание: решение задачи мы нашли на границе многогранника R.
При этом возможны варианты:
Единственному конечному решению соответствует вершина R, как в нашем примере. Решением может являться бесконечное множество точек на грани R, например, если бы ограничение q3 определяло бы прямую, параллельную z (уравнения q3 и z были бы линейно зависимыми). Система ограничений может определять "открытый" многогранник R, включающий бесконечно удаленные точки, в которых достигается max z, т.е. max z = ?. Например, та же задача ЛП могла быть поставлена при отсутствии ограничений q2 и q3 (
рис. 4.2). Перемещение z в сторону ее увеличения может быть бесконечным, т.е. max z = ?. Но если бы была поставлена задача z


Рис. 4.2. Случай отсутствия решения
Значит, имеет значение, с какой стороны многогранник R открыт: либо он позволяет поиск решения вдоль "закрытых" стенок, либо допускает возможность "выпасть" за его пределы, искать решение в бесконечности.
Тогда, как бы мы могли искать решение нашей первоначально поставленной задачи ЛП?
Учитывая, что решение задачи — в одной из вершин R, мы сначала выпишем уравнения всех прямых, ограничивающих R, т.е. уравнения всех его границ:
x1 = 40
x2 = 30
x1 + x2 = 50
x1 = 0
x2 = 0
Для нахождения координат каждой вершины R решаем совместно пару уравнений прямых, образующих эту вершину, и находим значение z в найденной вершине:


Действительно, max z = 190 достигается в точке A.
Отметим возможноcть распараллеливания решения задачи на многопроцессорной ВС, точнее, ВС SPMD-технологии.
В трехмерном пространстве ограничения и условия образуют пространственный многогранник R, охваченный плоскостями-границами, записанными на основе ограничений и условий, где неравенства заменены равенствами, а каждая плоскость z = const, среди которых мы ищем решение, пересекает, "прорезает" его, деля на две части (
рис. 4.3).

Рис. 4.3. Задача линейного программирования в трёхмерной области
На рисунке иллюстрируется задача ЛП:
z=c1x1+c2x2+c3x3

при ограничениях
q1=a11x1+a12x2+a13x3

q2=a21x1+a22x2+a23x3

и при условии
x1



Две грани q1=b1 и q2=b2, ограничивают многогранник R — область возможных значений переменных сверху (спереди) и справа. Слева, внизу и сзади пространственный многогранник R ограничен условиями неотрицательности решения, ставшими ограничениями x1 = 0, x2 = 0, x3 = 0. Плоскость z=const пересекает многогранник R. Перемещая плоскость z параллельно себе, т.е. вдоль вектора (c1, c2, c3), в сторону возрастания значений линейной формы z, мы находим решение. Здесь наглядно показана очевидность того, что решение следует искать в вершинах R.
Однако графическое представление уже в трехмерном пространстве затруднительно, в n-мерном пространстве нам необходимо действовать формально. Здесь существует ряд проблем.
Во-первых, мы не представляем пространственной картины и не знаем, охватывают ли заданные ограничения область R со всех сторон и какими условиями эти ограничения должны быть дополнены без противоречий.
Во-вторых, мы не знаем, какие n ограничений, дополненных условиями, соответствуют каждой конкретной вершине многогранника R, чтобы найти координаты этой вершины и найти в ней значение целевой функции z. Значит, мы должны испытать все возможные комбинации по n (в данном случае — тройки) ограничений и условий, т.е. все возможные комбинации по три, составленные на основе всех потенциальных границ- ограничений и условий.
Тогда при построении (параллельной!) вычислительной процедуры мы должны опираться на то, что любая противоречивость в системе ограничений (в их состав мы включили теперь и условия) выразится в неразрешимости системы трех уравнений, составленной для нахождения координат очередной испытываемой вершины R. Т.е. в этом случае вершина находится в бесконечности или содержит отрицательные значения координат. Эта неразрешимость находится в процессе счета.
Оставаясь в области практических решений задач ЛП, т.е. в области инженерии и экономики, примем предположение, что задача сформулирована корректно. Под этим будем предполагать, что ограничения выбраны так, что она не имеет неограниченного решения z = ?.
Например, ставя задачу о максимизации прибыли от перевозки, не надо забывать о том, что объем перевозок ограничен ресурсами страны, сообщества и т.д. В противном случае мы получим тривиальное решение: чем больше, тем лучше.
Значит, мы будем предполагать, что в многограннике R обязательно есть вершины (их координаты не отрицательны), в целом ограничивающие области изменения переменных, и хотя бы в одной из этих вершин целевая функция — линейная форма z принимает максимальное значение.
В свете сказанного будем также считать, что ограничения не противоречивы. Противоречивые ограничения приводят к случаю R =

Например, ограничения
x + y

x + y

противоречивы.
Тогда, развивая на n-мерное пространство, мы можем реализовать следующую стратегию поиска решения задачи ЛП.
Общий алгоритм
Формируем систему m + n уравнений
 |
(4.13) |
действительных и возможных границ многогранника R допустимых решений. Эта система уравнений отображает m заданных ограничений и n условий неотрицательности решения.
Решая совместно подмножество n уравнений этой системы, находим одну из вершин X0 многогранника R. Находим значение z0
целевой функции в точке X0.
Дополним систему n уравнений, первоначально породившую вершину X0, теми уравнениями, которым X0 также удовлетворяет. Получим систему p

 |
(4.14) |
Примечание 1. Теперь наша задача — переместиться вдоль одного из ребер, исходящих из вершины X0, в смежную вершину X1, такую, что Z(X1) > Z(X0). При этом, желая ускорить процесс (хотя выбор стратегии нуждается в обосновании), будем среди всех смежных вершин искать ту вершину X1, в которой достигается максимальное увеличение значения целевой функции. Каждое ребро описывается системой n - 1 уравнений из состава p уравнений, породивших испытываемую вершину X0. Введем переменную p, первоначально приняв p = n
Выбирая из (4.14) по n - 1 уравнений, будем получать систему, которая определяет некоторое ребро, исходящее из X0. Всего таких подсистем может быть Cpn - 1.
Последовательно испытываем данное ребро на его пересечение с теми из m гранями из (4.13), которые не вошли в состав (4.14). Т.е. дополняем нашу систему n - 1 уравнений очередной испытываемой гранью. Получаем систему n уравнений и решаем ее. Возможны следующие варианты.
Система не имеет решения, имеет не единственное решение или решение содержит отрицательные компоненты. Переходим к испытанию следующей грани.
Система имеет неотрицательное решение, но это решение не удовлетворяет всем m ограничениям задачи, т.е. находится вне R. Переходим к испытанию следующей грани.
Система имеет неотрицательное решение X1

Если Z(X1) = Z(X0), запоминаем вершину X1. Это для случая, если в результате проводимых испытаний оказалось, что точка X0 — решение задачи. Тогда необходимо знать все вершины, образующие решение, чтобы построить общее параметрическое выражение. Переходим к испытанию следующего ребра. Если Z(X1) > Z(X0), запоминаем точку X1 в данном качестве и переходим к испытанию следующего ребра.
Примечание 2. Возможна стратегия, при которой смещение производится в первую же найденную вершину с превышающим значением целевой функции. Есть вариант, что это — более правильная стратегия, т.к. значительное увеличение значения целевой функции на данном шаге может привести в дальнейшем к увеличению числа шагов: мы ничего не знаем о особенностях многогранника решений. Мы же здесь рассматриваем стратегию, при которой отыскивается смежная вершина с максимальным превышением целевой функции.
Перебрав все грани для одной подсистемы n - 1 линейных уравнений (для одного ребра), формируем другую подсистему таких уравнений на основе (4.14). Анализируем ее совместно со всеми m + n - p уравнениями из (4.13).
Таким образом, исследовав все ребра, исходящие из X0, мы можем найти ту смежную вершину X1, где целевая функция максимально превышает ее значение в исходной вершине. Перемещаемся в эту вершину, полагая X0 = X1. Система (4.14) теперь — та система n уравнений, решение которой породило X1. Дополняем ее уравнениями других граней, проходящих через X1. Получаем p

Если не удается найти вершину, в которой значение целевой функции превышает ранее найденное, то мы нашли решение. Одновременно мы нашли и сохранили те смежные (проанализированной вершине!) вершины, в которых значения целевой функции равны. Однако мы могли найти не все вершины, обладающие одним, максимальным, значением Z.
Ведь мы двигались только по ребрам, исходящим из предыдущей анализируемой вершины. "Напротив" этой вершины могут быть другие вершины с тем же значением целевой функции, и в эти вершины не ведут ребра из данной. Однако на основе свойств выпуклого многогранника можно заключить, что отношение взаимной смежности связывает все вершины, образующие решение задачи ЛП. Т.е. вершины-решения, не смежные друг другу, являются смежными другим вершинам-решениям. Существует путь вдоль ребер, связывающий вершины-решения. Тогда можно построить алгоритм выявления всех вершин R — решений задачи ЛП.
Пусть найденные уже вершины-решения образуют множество A. Дополним его последней найденной вершиной. Выбираем первую из ранее запомнившихся вершин из A с равным, максимальным, значением целевой функции и делаем ее опорной, X0.
Выполняем шаги 4-8 для поиска вершины многогранника R с более высоким значением Z, чем значение Z(X0). Конечно, мы такой вершины найти не можем. Но мы можем найти новую вершину X, не входящую в множество A, такую, что Z(X) = Z(X0). Включаем вершину X в A, полагаем X0 := X. Продолжаем выполнение данного пункта до тех пор, пока множество A не перестанет пополняться новыми вершинами. Производим параметрическую запись (4.4) общего решения задачи.
Общий алгоритм перебора
На основе ограничений задачи q1


= 0, ... , xn = 0. Получим систему m+n линейных уравнений, в общем случае избыточную и, возможно, противоречивую.
Выбираем из этой системы очередную подсистему n линейных уравнений (всего таких подсистем Cnm + n) и решаем ее.
Как известно, система n линейных уравнений имеет единственное решение в том и только в том случае, если ранг r матрицы системы равен рангу расширенной матрицы системы и равен n.
Можно в вычислительную процедуру включить анализ соответствующих матриц. Можно ограничиться анализом только определителя системы, его отличием от нуля, т.к. нас интересует лишь единственное решение. Однако ориентация на современные вычислительные средства и их операционные системы позволяет этого не делать.
Дело в том, что любой метод решения системы линейных уравнений в случае неразрешимости системы или неоднозначности решения столкнется с операцией деления на нуль — т.е. возникнет прерывание. Этим целесообразно активно пользоваться для упрощения вычислительной процедуры.
После обработки прерывания необходимо предусмотреть переход к решению следующей, очередной подсистемы линейных уравнений, если такие еще не исчерпаны.
Однако традиционно при решении систем линейных уравнений в подобных задачах используют метод Гаусса как обобщение метода последовательного исключения. Метод Гаусса позволяет получать значения переменных последовательно. Значит, их контроль на отрицательность производится немедленно и останавливает дальнейший счет. Кроме того, попутные преобразования системы уравнений позволяют динамически выявить тот случай, когда матрица — алгебраическое дополнение диагонального элемента содержит нулевую строку, т.е. определитель системы равен нулю. Это также останавливает дальнейший анализ системы уравнений.
Если же получено единственное решение и все его компоненты x1, ... , xn не отрицательны, то они могут определять вершину многогранника R.
Могут, ибо если среди уравнений подсистемы есть уравнения вида xj = 0, введенные в состав граней на основе условий неотрицательности решений, и не вошли все уравнения граней, обусловленные ограничениями задачи, то полученное решение может противоречить некоторым "законным" ограничениям задачи. А именно — не представленным в составе решенной подсистемы.
Поэтому в таком случае необходимо дополнительно проверить, принадлежит ли действительно точка (x1, ... , xn) многограннику R, т.е. выполняются ли для нее все не отображенные в подсистеме ограничения вида qj

Если найденная точка (x1, ... , xn) действительно является вершиной многогранника R, определяемого ограничениями и условиями при постановке задачи, отыскивается значение z(x1, ... , xn) = c1x1+c2x2+ ... +cnxn. Если это значение превосходит ранее полученные при уже проведенном анализе других вершин, оно запоминается вместе со значениями x1, ... , xn — для продолжения поиска и анализа других вершин R или окончания решения задачи. Перебор всех подсистем n линейных уравнений на основе m+n ограничений (исходных и дополнительных), их число Cnm+n, полученные при их решении координаты вершин многогранника R, обусловленного числом m основных ограничений, позволяет выбрать ту вершину, которая порождает максимальное (минимальное) значение целевой функции — линейной формы z.
Данная вычислительная процедура хорошо реализуется на многопроцессорных ВС. Различные варианты подсистем линейных уравнений следует динамически распределять между процессорами. А это, в свою очередь, полностью соответствует SPMD-технологии "одна программа — много потоков данных".
О единственности решения. Мы видели по рисункам, что z = zmax может выполняться на ребрах и гранях многогранника R. Если на ребре, то в двух сопряженных вершинах z принимает одинаковое значение zmax. Если на гранях, то более чем в двух вершинах z = zmax . Это легко переносится в n-мерное пространство.
Итак, указанная вычислительная процедура может привести к получению единственной вершины X = (x1, ... , xn) многогранника R, в которой z(X) = zmax.
Пусть в r вершинах X1, ... , Xr многогранника R выполняются равенства z(Xj) = zmax, j = 1, ... ,r. Построим выпуклую комбинацию векторов:
X = k1 X1 + k2 X2 + ... + kr Xr , k1 + k2 + ... + kr = 1, kj

Множество значений X, удовлетворяющих этому условию, определяет бесконечное множество решений данной задачи ЛП.
Легко видеть, что данная вычислительная процедура предполагает любое соотношение n

Параллельное решение задачи целочисленного линейного программирования
Методы параллельного решения задачи ЛП, основанные на непосредственном перемещении по ребрам многогранника решений, не привлекая дополнительных переменных, способствуют построению наглядного метода решения соответствующей задачи линейного программирования (задачи ЦЛП). Под соответствием мы понимаем добавление условия целочисленности решения при той же формальной постановке задачи ЛП.
Такой метод основан на захвате в "вилку" некоторой целой точки внутри многогранника решений, вблизи точки решения задачи ЛП.
Рассмотрим пример.
Решим задачу ЦЛП:
Z = x - 3y + 3z

при ограничениях
2x + y - z

4x - 3y

-3x + 2y + z

и при условиях x, y, z

Решение задачи ЛП достигается (рис. 4.5) в точке (0,5, 0, 7,5), которая является результатом решения системы уравнений — граней
q2 = 4x - 3y - 2 = 0
q3 = -3x + 2y + z - 6 = 0
q5 = y = 0
Значение целевой функции Z(0,5, 0, 7,5) = 23.

Рис. 4.5. Решение задачи целочисленного линейного программирования
Положим ? Z = 4, и найдем все точки пересечения образовавшейся "целевой плоскости" с ребрами, исходящими из вершины-решения. Для ребра (q2, q3)

Все координаты при переходе из вершины-решения в найденную точку превысили некоторые целые значения. Причем, одна из координат "преодолела" именно ближайшее целое, заставив другие координаты "преодолеть" большее число единиц.
Для ребра (q2, q5)

Не все координаты "преодолели" ближайшее целое значение: x остался внутри интервала (0, 1).
Для ребра (q3, q5)

Опять не все координаты "преодолели" ближайшее целое: x остался внутри интервала (0, 1).
Значит, только в точке

наблюдается "преодоление" целых значений по сравнению с точкой (0,5, 0, 7,5), представляющей точное решение задачи ЛП. Т.е. нам удалось захватить решение задачи ЦЛП в "вилку". При этом точка (2, 2, 8), "преодоление" которой произошло, — возможное решение задачи ЦЛП.
Однако для того, чтобы координате z преодолеть ближайшее целое значение, координатам x и y пришлось преодолеть по два целых значения. Поэтому закономерен вопрос о том, нет ли внутри отсеченной с помощью ? Z области целых точек, где z преодолевает ближайшее целое с меньшей ценой для других координат. Ведь значение целевой функции в таких точках было бы больше.
Половиним "вилку". Положим ? Z = 2 и найдем точки пересечения "целевой плоскости" Z = 21 c ребрами, исходящими из вершины-решения задачи ЛП:

Видим, что есть координата,

Вновь половиним "вилку" в сторону увеличения значения ? Z, пытаясь вплотную подойти к возможной целой точке, где значение Z максимально. Положим ? Z = 3. Найдем точки пересечения "целевой плоскости" Z = 20 с ребрами, исходящими из вершины-решения задачи ЛП.
Решаем первую систему.

Решение "преодолело" целые значения по всем координатам. Не менее чем по одной координате произошло округление до ближайшего целого. Более того, по всем координатам получены целые значения. Дальнейший поиск прекращается, решение задачи ЦЛП найдено.
Если бы решение не совпало с целым, мы проверили бы точки пересечения "целевой плоскости" с другими ребрами. Вместе с тем, это можно и не делать, т.к. для меньшего значения Z = 19 уже установлен факт "непреодоления" там целых значений. Так что нам осталось бы только выполнить округление.
Рассмотренные в лекции методы решения задач линейного программирования имеют важную методологическую направленность, обусловленную наглядностью, ощутимостью, чувством "физического смысла" задач. Их роль не осмысленна до конца, но они позволяют эффективно распараллеливать вычисления. В этом смысле такие методы, как симплекс-метод, венгерский метод ориентированы исключительно на последовательные вычисления, но зато полностью исключают перебор. Для большой размерности задачи введение дополнительных переменных, что предполагается в симплекс-методе, может показаться нежелательным.
Предложен вполне практический метод (хотя и не описан алгоритмически) решения задачи ЦЛП, опирающийся на нахождение хотя бы одного решения соответствующей задачи ЛП. Мы не затронули вопроса о единственности решения — как задачи ЛП, так и задачи ЦЛП, о произвольном числе ребер, образующих вершину-решение задачи ЛП. Метод, несомненно, подлежит развитию. Его достоинство заключается в том, что он, по сравнению с методом "ветвей и границ", не требует многократного решения задачи ЛП с динамически уточняющимися и размножающимися ограничениями.
Можно указать на осуществляемое практическое применение предлагаемых методов в качестве тестовых задач для оценки эффективности многопроцессорных ВС, использующих принципы SPMD-технологии ("единственная программа — много потоков данных"). Эти же методы используются при разработке сетевых технологий решения сложных задач.

План параллельных вычислений
Воспользуемся в основном той же схемой вычислений, что и в разделе 4.1.
Пусть все процессоры ВС или используемые станции локальной сети обладают своим номером и знают количество используемых средств. Как показывалось ранее, они все начинают решать "свои" системы линейных уравнений. Здесь уже можно применить различные стратегии. Одна из них: пусть хотя бы один процессор нашел вершину многогранника R. Ее можно взять за вершину X0.
Другая стратегия заключается в том, чтобы дать возможность всем участвующим процессорам найти по одной вершине R. Вершину с максимальным значением целевой функции Z можно взять за X0.
Выбрав вершину X0, все процессоры начинают решать "свои" варианты систем линейных уравнений в поисках смежных вершин с превышающим значением целевой функции. Согласовав действия при нахождении вершины X1 и приняв X0 := X1, они продолжают процесс движения по ребрам R.
Предпосылки методов
Задачи линейной и нелинейной оптимизации, сетевые транспортные задачи — задачи высокой сложности, подверженные "проклятию размерности". Ориентация на применение многопроцессорных симметричных вычислительных систем в составе персональных компьютеров или рабочих станций (параллельные вычисления) и на применение сетевых технологий (распределенные вычисления) требует разработки новых параллельных методов их решения. Эти методы должны быть лишены недостатков "традиционных" методов: последовательного характера вычислений и введения дополнительных переменных (для задач линейного программирования). Анализ способов распараллеливания показывает эффективность распараллеливания "по информации". Весьма перспективной поэтому становится SPMD-технология программирования (Single Program — Multiple Data). При этой технологии вычислительный процесс строится на основе единственной программы, запускаемой на всех процессорах вычислительной системы или на многих станциях локальной сети. Копии программы могут выполняться по разным ветвям алгоритма, обрабатывая подмножества данных. Неизбежна синхронизация во времени и при обработке общих данных.
Такая технология параллельного программирования и обусловила разработку рассмотренных ниже методов. В то же время не отрицаются известные традиционные методы, сокращающие общее число операций и исключающие перебор. Иной методологический подход открывает дорогу решению задач большой размерности и эффективной параллельной работе многих процессоров. Для ряда задач этот подход еще нуждается в исследовании, уточнении области применения и развитии — проведении тщательной математической экспертизы. Поэтому мы посчитали необходимым осветить его подробно — для лучшего представления "физического смысла", ощутимости пространственной модели задач и следующих из этого планов их параллельного решения.
допустимых решений, представленный на рис.
Рассмотрим задачу линейного программирования
Z = 26x + 20y + 21z

при ограничениях
q1 = 2x + 7y - 76z + 222

q2 = - 8x +9y - 8z + 64

q3 = - 8x + 13y -24z + 96

q4 = - x - 6y - z + 70

q5 = - 2x - 7y - 2z + 90

q6 = 33x + 3y +22z - 165

и при условии x



0.
Ограничения и условия образуют многогранник R(ABCDEFGHKL) допустимых решений, представленный на рис. 4.4.
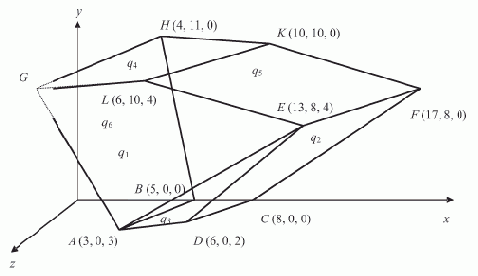
Рис. 4.4. Многогранник допустимых решений
Формально мы не знаем R, и множество граней — действительных и возможных — этого многогранника представлено системой уравнений:
q1 = 2x + 7y - 76z + 222 = 0
q2 = - 8x +9y - 8z + 64 = 0
q3 = - 8x + 13y -24z + 96 = 0
q4 = - x - 6y - z + 70 = 0
q5 = - 2x - 7y - 2z + 90 = 0 (4.8)
q6 = 33x + 3y +22z - 165 = 0
q7 = x = 0
q8 = y = 0
q9 = z = 0
В результате решения первой же подсистемы трех уравнений (n = 3) системы (4.8) получаем координаты вершины E многогранника R
 | (4.9) |
Постараемся "сместиться" в ту вершину, смежную вершине E, т.е. соединенную с ней ребром (в одну из вершин A, D, L, F), в которой целевая функция Z имеет максимальное значение, превышающее Z(E).
Ребра, исходящие из вершины, определяются подсистемами n-1 плоскостей, пересекающихся в этой вершине, т.е. образующими ее.
В данном случае подсистема


определяет ребро EA, подсистема

определяет ребро ED. А вот ребра EL и EF мы пока не знаем, т.к. не знаем (формально, а не по рисунку!) все плоскости (плоскость q5), пересекающиеся в E. Это значит, что из каждой вершины в общем случае исходят не менее n ребер, а сколько в действительности — предстоит уточнить. (Представьте себе R — бриллиант классической огранки.)
Значит, q1, q2, q3 — это лишь наше начальное представление о множестве плоскостей — граней, пересекающихся в вершине E. Нам необходимо развить это представление до полного.
Тогда выясним все множество граней, образующих вершину E, подстановкой ее координат во все другие уравнения (9.8) и испытанием на получение тождества.
Находим q5(13, 8, 4)

 | (4.10) |
Каждую возможную грань, определяемую двумя (n-1) уравнениями плоскостей из (4.10), будем решать совместно со всеми плоскостями из (4.8), не вошедшими в (4.10), — с гранями q4, q6, q7, q8, q9.
Первая такая система имеет вид
 | (4.11) |
Ее решение (535, 8,7, -517,2) содержит отрицательную составляющую. Т.е. эта точка не принадлежит R. Если бы решение было не отрицательным, мы должны были бы проверить выполнение всех ограничений (4.7), не представленных в (4.11).
Можно показать, что в выпуклом многограннике несуществующее ребро не вызовет появления "ложной" вершины, и достаточно проверить (4.7).
Системы

имеют не положительное решение.
Следующая испытываемая система линейных уравнений на основе двух уравнений из (4.10) и не входящих в (4.10) уравнений из (4.8), имеет вид

Ее решение — приблизительно точка (5,2, 9,4, 4) не является вершиной R, т.к. не удовлетворяет всем ограничениям (9.7), q5(5,2, 9,4, 4) < 0.
Следующая испытываемая система имеет вид

Ее решением является вершина A (3, 0, 3), Z(A) = 141 < 592.
Т.к. мы нашли вершину на "другом конце" ребра, анализ данного ребра прекращаем.
Следующее исследуемое ребро, исходящее из вершины E, определяется подсистемой

которая должна решаться совместно с уравнениями q4 = 0, q6 = 0, q7
= 0, q8 = 0, q9 = 0.
Первая же система

Следующее возможное ребро, исходящее из вершины E, определяется комбинацией

Решая ее совместно с другими гранями R, - q4 = 0, q6 = 0, q7
= 0, q8 = 0, q9 = 0, пытаемся найти другую вершину в R, смежную E.
Очередная решаемая система уравнений

имеет не отрицательное решение (13,625, 8,7, 4,175). Проверяем выполнение ограничений (9.7), не представленных в решенной системе. Находим, что q1(13,625, 8,7, 4,195) < 0. Этой проверки достаточно для вывода о том, что найденная точка не является вершиной многогранника R.
Системы

и

имеют решение в отрицательной области.
Система

определяет вершину D (6, 0, 2), для которой Z(D) = 198 < 592.
Следующее возможное ребро по (4.10) определяется парой граней

Решаем совместно с остальными гранями, не входящими в (10): q4 = 0, q6 = 0, q7 = 0, q8 = 0, q9 = 0.
Система

не имеет решения, ранг матрицы системы не равен рангу расширенной матрицы.
Система

имеет отрицательное решение.
Система

имеет неотрицательное решение, при котором q1 < 0. Найденная точка не является вершиной R.
Система

не имеет решения.
Система

имеет неотрицательное решение — точку F (17, 8, 0), удовлетворяющую всем ограничениям: q1(17, 8, 0) > 0, q3 (17, 8, 0) > 0, q4(17, 8, 0) > 0, q6(17, 8, 0) > 0. Точка F — вершина многогранника R. Z(F) = 602 > 592.
Таким образом, мы нашли вершину F, смежную вершине E, с превышающим значением целевой функции. Однако поиск всех вершин на основе (4.10), смежных вершин E, следует продолжить. Ведь формально возможна и другая вершина, с еще большим значением целевой функции.
Перебор продолжаем на основе ребра

хотя мы видим по рисунку, что такого ребра нет.
Ищем точки пересечения этого ребра со всеми гранями R, не вошедшими в (4.10).
Система уравнений

имеет решение (0,875, 10, 9,125).
При проверке выполнения первого же ограничения оказывается, что q1(0,875, 10, 9,125) < 0. Найденная точка действительно не является вершиной R.
Система

имеет отрицательное решение.
Система

имеет решение (0, 10,144, 9,5), не удовлетворяющее первому же ограничению.
Система

имеет отрицательное решение.
Система

имеет не отрицательное решение (22,96, 6,44, 0), не удовлетворяющее ограничениям.
Таким образом, анализ всех возможных вершин, смежных вершине E, закончен. Мы нашли единственную вершину F(17, 8, 0), где значение целевой функции Z(17, 8, 0) = 602 превышает ее значение в точке E. Система уравнений, определившая эту вершину, имеет вид
 | (4.12) |
Если бы мы нашли несколько вершин с одинаковым значением целевой функции, то были бы возможны различные стратегии дальнейших действий.
Мы здесь рассматриваем случай, когда для дальнейшего поиска фиксируется одна из таких вершин. Других граней, которым принадлежит точка F, нет. Смещаемся в эту вершину, полагаем p = 3.
Начинаем весь процесс поиска смежной вершины с максимальным (среди смежных вершин) значением целевой функции Z, обязательно превышающим значение Z(F).
Первое возможное ребро, исходящее из F, определяется уравнениями

Однако эта комбинация возвращает нас в ту вершину, которую мы уже исследовали. Поэтому сразу же переходим к следующему возможному ребру

решая его совместно с гранями q1, q3, q4, q6, q7, q8.
Система

решалась ранее. Ее решение неположительно. (Если мы переупорядочим уравнения системы по индексам, то получим индексный код, по которому будем входить в таблицу с информацией о решенной ранее системе. Так мы реализуем самообучение в процессе решения.)
Система

решалась ранее. Ее решение также содержит отрицательный компонент.
Система

решается впервые. Ее не отрицательное решение не удовлетворяет всем ограничениям, q3(17,8, 8,7, 0) < 0.
Системы

и

имеют решения, содержащие отрицательные компоненты.
Система

определяет вершину C, Z(8, 0, 0) = 208 < 602.
Следующее исследуемое ребро определяется системой уравнений

Система

исследовалась раньше. Она не имеет решения.
Система

решалась ранее. Она определяет точку, не являющуюся вершиной R.
Система

решается впервые. Она определяет точку K. Однако Z(10, 10, 0) = 460 < 602.
Таким образом, нам не удалось сместиться из вершины F в вершину с большим значением Z. Значит, найденная точка F определяет решение задачи ЛП.
Пример применения параллельной процедуры прямого перебора
Решим ту же задачу (2), подойдя формально, по правилу, пригодному для любой размерности пространства.
Исходная система уравнений действительных или потенциальных плоскостей — граней R имеет вид
 |
(4.4) |
Т.к. C23+2=10, исследование десяти комбинаций (подсистем уравнений) по два уравнения из (9.4) выглядит следующим образом.

Подставляем это уже готовое решение в третье ограничение задачи, x1+ x2


Решение удовлетворяет третьему ограничению x2

Находим и запоминаем z(40, 10) = 130.

Система не имеет решения.

Решение удовлетворяет ограничениям

Находим z(40, 0) = 80. Если мы решаем задачу не на параллельном компьютере, то сразу же видим, что новое значение z не превосходит уже найденное. Поэтому и это решение отвергаем.

Решение x1 = 20, x2 = 30 удовлетворяет и третьему "основному" ограничению задачи x1


Решение удовлетворяет всем ограничениям задачи. z(0, 30) = 150, что не превосходит уже найденное значение. Решение отвергаем.

Не имеет решения.

Решение x1 = 0, x2 = 50 противоречит "основному" ограничению x2


Решение x1 = 50, x2 = 0 противоречит "основному" ограничению x1


Решение не противоречит "основным" ограничениям задачи. Однако z(0, 0) = 0, что не превосходит уже найденное значение. (Кстати, оно обеспечивает решение задачи z

Итак, x1 = 20, x2 =30 обеспечивает zmax =190, т.е. является решением задачи ЛП.
Сложность алгоритма
Если считать, что чаще всего из одной вершины исходят n граней, то число решаемых систем n линейных уравнений при поиске смежных вершин определяется как
r = n ? (m + n - n) = n ? m.
Число вершин k, по которым производится перемещение в поисках решения, предсказать трудно. Однако очевидно, что k << Cnm + n, т.к. лишь локально затрагивается некоторый "бок" многогранника R. Считая, как и раньше, m

Сложность алгоритма прямого перебора
Основным элементом решаемой задачи является решение системы n линейных уравнений. Сложность решения такой системы можно считать полиномиальной O(n3). Число решений определяется как Cnm+n. Чтобы найти зависимость сложности от основных параметров n и m, определим, во сколько раз увеличивается сложность при увеличении размерности n на единицу:
 |
(4.5) |
Если считать, что m соразмерно с n, т.е. m

Простота параллельного алгоритма прямого перебора делает его привлекательным для значений n порядка двух-трех десятков. Для большей размерности необходимо искать алгоритмы полиномиальной сложности.
Алгоритм
Пусть стек составляют нуль-единичные строки длины n (число каналов сети). Для каждой строки известно упорядоченное по номерам множество M каналов, логическая сумма строк которых в матрице S определила данную строку. Номер k последнего канала в этом множестве известно. Для каждой строки известен последний испытанный нулевой элемент.
Загружаем очередную i -ю, i = 1, ... ,n-1, строку в стек. Полагаем M ={i}, k = i. В строке-вершине стека находим очередной нуль, занимающий позицию j > i. Переходим к выполнению шага 4. Если такого нуля нет, или все они испытаны, строку исключаем из стека. Если после этого стек исчерпан, выполняем шаг 1. В противном случае выполняем шаг 2. Складываем логически строку из вершины стека со строкой j — формируем новую вершину стека. Номером канала j дополняем множество каналов M, участвующих в формировании новой строки. Полагаем k = j. Если в строке-вершине стека все нули соответствуют только всем каналам в M, то M — очередное найденное ПМВНК. Фиксируем это множество. В любом случае исключаем строку-вершину стека из стека. Выполняем шаг 2.
Исходные построения
Исследование потоков в сети — важная, всегда актуальная задача исследования операций. Она лежит в основе моделирования при проектировании как транспортных сетей, так и сетей водоснабжения и канализации. Известен ряд классических моделей (приводимых, например, в [15]) в этой области. Важнейшую роль играют модели, позволяющие определить "узкие" мести сети. Они определяют ее максимальную пропускную способность между выделенными пунктами, или, иначе говоря, ее минимальное сечение. Это задача дискретного программирования, широко использующая перебор и относящаяся к задачам высокой сложности.
При аналитическом моделировании сети используется известный [15] алгоритм Форда-Фалкерсона.
Теория параллельного программирования способна предложить более простой алгоритм перебора. Его достоинством является параллелизм, который позволяет эффективно использовать многопроцессорные ВС и вычислительные комплексы на основе рабочих станций локальной сети. Возможен наиболее простой способ распараллеливания на основе применения SPMD-технологии.
Пусть задана сеть (рис. 5.1). Дуги ее назовем каналами. Каналы пронумерованы. Направление потоков показано стрелками. Вершины — точки сопряжения каналов, вершина A — исток, вершина B — сток. Каждая дуга i сопровождается информацией об интересующих нас характеристиках потока, например, о пропускной способности di канала. В этом случае правомерен вопрос о максимальной пропускной способности сети, обусловленной минимальным сечением.

Рис. 5.1. Сеть для оценки пропускной способности
В терминах теории параллельного программирования (лекция 7) каждое сечение сети (например, сечение, пересекающее каналы 1, 2, 4, 7) является полным множеством взаимно независимых работ — каналов (ПМВНК). Перебрав все такие множества и рассчитав для каждого суммарную пропускную способность, мы можем найти минимальное значение. Оно характеризует минимальное сечение, а следовательно, максимальный возможный поток в сети.
В [3] приводится алгоритм перебора всех полных множеств взаимно независимых работ.
Усовершенствуем его, получая такие множества, упорядоченные по номерам каналов, и исключая повторное нахождение одних и тех же полных множеств. (В лекции 7 изложенные ниже преобразования будут рассмотрены глубже.)
Построим треугольную матрицу следования S, отражающую граф сети (рис. 5.2а). Сложив каждую последующую строку с теми предыдущими, которые соответствуют единичным элементам этой строки, получим матрицу следования S с транзитивными связями (рис. 5.2б). Транспонируем матрицу S и объединим с ее начальным видом (рис. 5.2в). Иначе, отобразим S симметрично относительно главной диагонали. Получим матрицу S, отображающую как порядок следования, так и порядок предшествования каналов.

Рис. 5.2. Полная матрица следования каналов:а — начальный вид, б — дополнение транзитивными связями, в — конечный вид
Теперь матрица S полностью отражает взаимную независимость каналов. Например, если сложить логически строки 1, 2, 3, то получим строку, содержащую нули только в позициях 1, 2, 3. Тем самым мы получим ПМВНК {1, 2, 3}. Множество полное, т.к. дополнительное сложение с любой другой строкой изменит состав нулей.
Таким образом, наша задача заключается в том, чтобы испытать все варианты сложения групп строк так, чтобы нули в строке-результате оказывались в тех и только в тех позициях, которые соответствуют строкам- слагаемым. Тогда эти строки определят очередное ПМВНК. Упорядочение по номерам строк поможет нам избежать повторного получения ПМВНК с другим порядком следования номеров каналов.
О применении схемы Гаусса решения систем линейных уравнений в транспортной задаче
Остался неясным вопрос: приходится ли в общем случае при решении систем линейных уравнений для данной задачи пользоваться схемой Гаусса, или достаточно последовательно пользоваться простыми подстановками?
Подстановки мы легко выполняли в том случае, если в результате введения нулевых комбинаций у нас получались уравнения, содержащие в левой части единственную переменную. Если таких уравнений нет, то очевидна целесообразность применения схемы Гаусса.
Тогда выясним, существует ли комбинация нулей, такая, при которой в каждой строке A, с учетом неисключенной строки, остается не менее двух единиц.
Рассмотрим только n = 4 последних уравнений из (5.6): три последних уравнения из (5.7) и уравнение y4 + y8 + y12 = 7. Их матрица имеет вид

Т.е. она состоит из m матриц с единицами по главной диагонали. Чтобы в одной строке такой матрицы остались хотя бы две единицы, необходимо оставить невычеркнутыми хотя бы два столбца. В другой строке должны быть не вычеркнуты хотя бы два обязательно других столбца. Итого, для четырех строк примера должны остаться невычеркнутыми восемь различных столбцов. Значит, вычеркнуть мы можем только четыре столбца (например, как выделено на изображении матрицы), а нам надо положить равными нулю шесть переменных! Тем самым, на базе лишь этих "нижних" уравнений образуются не менее двух уравнений с единственной переменной в левой части.
Т.к. произведение m ? n растет значительно быстрее суммы m + n, то с ростом параметров задачи указанное свойство усугубляется. Следовательно, мы с полным основанием может рассчитывать на принцип подстановки, как мы и делали в примере.
Однако программирование схемы Гаусса может оказаться не только менее трудоемко. Не следует забывать, что в процессе преобразования системы уравнений и последовательного получения значений переменных оперативно устанавливается как неразрешимость или неоднозначность, так и отрицательное решение.
Например, система (5.17) при реализации схемы Гаусса проходит следующие стадии преобразования.
Вычитание первой строки из последней и формирование разности на месте второй строки:

Вычитание пятой строки из третьей и размещение разности на месте четвертой строки:

Сложение шестой строки с пятой и расположение разности на месте пятой строки:

Получение нулевой строки в матрице достаточно для заключения о непригодности решения (в данном случае оно не существует).
Рассмотренная транспортная задача, без ограничения пропускной способности транспортных потоков, демонстрирует параллельный алгоритм ее решения. Программа, одинаковая для всех процессоров многопроцессорной ВС или станций локальной вычислительной сети, в основной своей части реализует выборку очередного ребра, исходящего из первоначально найденной вершины многогранника решений. Вдоль него ищется смежная вершина с меньшим значением целевой функции. Процессор, нашедший такую вершину, производит замену ранее исследовавшейся вершины и вынуждает все процессоры приступить к анализу ребер, исходящих из новой вершины. Так — до неудачного поиска вершины с меньшим значением целевой функции.
Использование в качестве источника загрузки процессоров общей уточняемой базы данных, в которой хранятся исследованные варианты поиска, позволяет выявлять еще не исследованные варианты и равномерно распределять нагрузку между процессорами.
Параллельное выполнение алгоритма
Предпочтительным способом распараллеливания здесь является распараллеливание по информации. Наиболее простая реализация его может быть основана на распределении между процессорами или станциями локальной сети строк матрицы S. И здесь самую простую реализацию предлагает принцип SPMD — "одна программа -- много потоков данных". Однако, как видно из примера, объем работ, связанных с разными строками, может быть весьма различным. Например, мы долго обрабатывали первую строку и быстро справились с такими строками, как 7, 8, 9. Значит, жесткое априорное распределение строк нежелательно. Оно обеспечивает неравномерную загрузку процессоров. Необходимо производить загрузку процессоров динамически, по мере их освобождения.
Здесь может быть эффективен тот же принцип, который используется при обработке баз данных, баз знаний и списковых структур.
Его реализация может быть следующей.
В соответствии с SPMD-технологией каждый процессор (станция локальной сети), участвующий в счете, обладает своим номером и знает количество процессоров. Множество строк матрицы S также упорядочено. Первоначально первый процессор выбирает для обработки и метит первую строку, второй — вторую и т.д.
По мере освобождения каждый процессор обращается к матрице S и выбирает первую из неотмеченных строк. Для согласованного обращения к S организуется синхронизация с помощью семафора методом взаимного исключения.
Сеть, в т.ч. транспортная, представляет собой параллельную структуру. Методы параллельного программирования предлагают эффективные средства для исследования сетей. Достоинством их является то, что сами эти методы допускают весьма простые способы распараллеливания. Это очень важно при обработке сетей большой размерности. Использование SPMD- технологии способствует эффективному применению многопроцессорных систем — внешних устройств персонального компьютера или множества станций локальной сети для решения задач высокой сложности.
Рассмотренные параллельные методы решения некоторых задач на транспортных сетях ориентированы на "прорыв в размерности", на выход на большие размерности задач, на задачи высокой, даже — экспоненциальной сложности. Только параллельные вычислительные системы могут решать такие задачи. Здесь очень важна концепция перспективных вычислительных средств: только ли разработка супер-ЭВМ призвана удовлетворить высокие требования по производительности? Не находятся ли на наших столах распределенные вычислительные комплексы РС, объединенные в локальные сети на основе современных, уже достаточно оперативных сетевых технологий? Именно для ответа на эти вопросы и должны критически перерабатываться и вновь создаваться параллельные алгоритмы решения сложных задач.

Параллельный алгоритм решения
Исследование плана параллельного решения и формирование алгоритма будем сопровождать примером, для проверки правильности заимствованным в [15]. Для краткости условия (5.3) и (5.4) опущены.
Пример.
Z=7x11+8x12+5x13+3x14+2x21+4x22+5x23+ +9x24+6x31+3x32+1x33+2x34

при ограничениях
x11 + x12 + x13 + x14 = 11
x21 + x22 + x23 + x24 = 11
x31 + x32 + x33 + x34 = 8
x11 + x21 + x31 = 5 (5.6)
x12 + x22 + x32 = 9
x13 + x23 + x33 = 9
x14 + x24 + x34 = 7
Введем линейный массив переменных xij = yk, где k = (i - 1)n + j.
Исключим из рассмотрения последнее уравнение. Система уравнений граней (действительных и возможных) многогранника решений примет вид
y1 + y2 + y3 + y4 = 11
y5 + y6 + y7 + y8 = 11
y9 + y10 + y11 + y12 = 8 (5.7)
y1+y5+ y9=5
y2+y6+y10 = 9
y3+ y7+ y11 = 9
yk = 0, k = 1, 2, ... , 12.
Итак, на первом этапе задача свелась к выбору и анализу комбинаций по 12 - 6 = 6нулевых значений координат искомой вершины многогранника решений. Выполняя подстановку выбранной комбинации в (5.7), мы можем решить образовавшуюся систему шести уравнений с шестью неизвестными. Таким образом, мы сможем найти координаты некоторой вершины.
Комбинации по шесть нулевых значений координат ("комбинации нулей") следует выбирать так, чтобы не обратилась в нуль левая часть хотя бы одного уравнения (5.7), включая исключенное уравнение. Например, комбинация, где y1 = y2 = y3 = y4 = 0, недопустима.
Найдем дополнительные контрольные ограничения: чтобы решение было не отрицательным, необходимо, чтобы любое значение yk, k = 1, ... , m ? n, не превышало значение yk — величины правой части того уравнения, в котором оно участвует.
Тогда в нашем примере y1












y12 = 7. Здесь при оценке y4, y8, y12учтено последнее уравнение в (5.6).
Воспользуемся векторной формой представления, чтобы подготовить удобные, нетрудоемкие матричные преобразования. А именно, наша система m + n - 1линейных уравнений-ограничений имеет вид
AY = B,
где A— нуль- единичная матрица, Y— столбец переменных, B— столбец свободных членов:
 | (5.8) |
Положим l = 0. Положим l := l + 1, yl = 0. Исключим из матрицы A столбец, соответствующий этой переменной. Проверяем, появилась ли в A строка, содержащая только нулевые элементы, или обратилась ли в нуль левая часть исключенного уравнения. (Предполагаем, что все свободные члены уравнений больше нуля.) При положительном результате анализа выполняем шаг 5. В противном случае — следующий шаг. Для каждой s-й строки A выделяем множество {ys}переменных, соответствующих единичным элементам. Проверяем:

Продолжим рассмотрение примера.
Полагаем y1 = 0. Это не приводит к нарушению оценок, указанных в алгоритме.
Полагаем y2 = 0. Это также не приводит к нарушению оценок.
Полагаем y3 = 0. Нулевые строки не появились. Однако в первой строке осталась единственная единица, соответствующая переменной y4. Т.к. y4= 7 < 11, отвергаем нулевое значение переменной.
Полагаем y4 = 0. Нулевые строки не появились, однако в первой же строке осталась единственная единица, соответствующая переменной y3. Т.к. y3 = 9 < 11, отвергаем и это значение.
Полагаем y5 = 0. Это не приводит к нарушению оценок.
Полагаем y6 = 0. В пятой строке остается единственная единица, соответствующая y10. Т.к. y10 = 8 < 9, отвергаем нулевое значение переменной.
Полагаем y7 = 0, что не приводит к нарушению оценок.
Значение y8 = 0 приводит к нарушению оценки во втором уравнении.
Значение y9 = 0 приводит к появлению нулевой строки.
Значение y10 = 0 не приводит к нарушению оценок.
Значение y11 = 0 также не приводит к нарушению оценок.
Итак, комбинация нулей найдена. Это отмеченные в (5.8) значения
y1 = 0, y2 = 0, y5 = 0, y7 = 0, y10 = 0, y11 = 0. (5.9)
Для нахождения других значений переменных необходимо решить систему уравнений на основе (5.8), после исключения нулевых столбцов

Найдем все строки матрицы A, содержащие не более одного единичного элемента. Это строки, определяющие компоненты решения y3
= 9, y6 = 9, y9 = 5.
Выполним подстановку, последовательно находя в столбцах найденных переменных единицы (не более одной) и корректируя правые части вычитанием найденных значений. Строки и столбцы, соответствующие найденным значениям переменных, исключаем из матрицы A.
Такой прием подстановки можно повторять до исчерпания уравнений, содержащих в левой части единственную переменную.
В нашем примере после подстановки найденных значений в уравнения 1, 2 и 3 получаем систему

В ней все уравнения имеют единственную переменную. Они определяют решение y4 = 2, y8 = 2, y12 = 3.
Таким образом, нам не пришлось пока воспользоваться методом Гаусса, но мы нашли допустимое решение Y0 = (0, 0, 9, 2, 0, 9, 0, 2, 5, 0, 0, 3), для которого выполняются ограничения задачи. Вектор Y0 определяет некоторую вершину многогранника допустимых решений, со значением целевой функции Z(Y0) = 141.
Примем следующий план решения, соответствующий рассмотренному ранее плану параллельного решения задач линейного программирования.
Для перебора всех смежных вершин необходимо в комбинации нулей, определивших вершину Y0, поочередно исключать одно значение yr = 0 (это определит одно из исходящих ребер) и оставшуюся систему решать совместно поочередно со всеми другими уравнениями вида ys = 0, не входящими в комбинацию нулей. Этим мы будем совершать перемещение в смежные вершины. Находя значение Z для каждого такого решения Y1 там, где оно существует, можно найти вершину с меньшим значением целевой функции. "Перебравшись" в эту вершину (приняв ее за Y0 ), мы можем продолжить анализ смежных ей вершин и т.д.
Решение задачи найдено в том случае, если после перебора всех смежных вершин не отыскивается вершина с меньшим значением целевой функции.
Продолжим рассмотрение примера.
Итак, (5.8) — исходный вид системы уравнений, (5.9) — комбинация нулей ("отсутствующие" столбцы в (5.7) выделены), (5.8) и (5.9) определяют вершину Y0.
Исключим из (5.9) уравнение y1 = 0, а оставшуюся систему, с учетом остальных нулей из комбинации (5.9), будем решать совместно с уравнениями
y3 = 0, y4 = 0, y6 = 0, y8 = 0, y9 = 0, y12 = 0. (5.10)
Значит, в (5.8) положим первоначально y3 = 0 вместо y1 = 0. Левая часть шестого уравнения (последняя строка матрицы А) обратилась в нуль.
Положим y4 = 0 вместо y1 = 0. Получим систему

Из нее, как и ранее, за два шага подстановки находим y3 = 9, y6 = 9, y9 = 5, а затем — y1 = 2, y8 = 2, y12 = 3.
Таким образом, найдено новое допустимое решение Y1 = (2, 0, 9, 0, 0, 9, 0, 2, 5, 0, 0, 3). Однако Z(Y1) =149 > 141. Найденную вершину отвергаем. Вместе с тем, т.к. мы нашли вершину "на другом конце" анализируемого ребра, то и анализ этого ребра прекращаем.
Приступаем к анализу следующего ребра, исключив из (5.9) уравнение y2 = 0. Оставшуюся систему, с учетом остальных нулей из (5.9), будем решать совместно с теми же уравнениями (5.10).
Положим в (5.8) y3 = 0 вместо y2 = 0. Последняя строка матрицы A стала нулевой.
Замена y4 = 0 вместо y2 = 0 приводит к системе

На ее основе находим новый вектор — допустимое решение Y1 = (0, 2, 9, 0, 0, 9, 0, 2, 5, 0, 0, 3). Однако Z(Y1) = 151 > 141. Найденную вершину также отвергаем. Ребро исследовано полностью.
Исключим из (5.9) уравнение y5 = 0, а оставшуюся систему, с учетом остальных нулей из (5.9), будем решать совместно с теми же уравнениями (5.10).
Положим в (5.8) y3 = 0 вместо y5 = 0. Последняя строка матрицы A обратится в нуль.
Положим y4 = 0 вместо y5 = 0. В первом уравнении не выполняется ограничение по y3 (y3 = 9).
Положим y6 = 0 вместо y5 = 0. Пятая строка A обратилась в нулевую.
Положим y8 = 0 вместо y5 = 0.
Получим систему уравнений

Находим y3 = 9, y6 = 9 и после подстановки — y4 = 2, y5 = 2. Вновь выполняем подстановку, находим y9 = 3, и после следующей подстановки y12 = 5.
Итак, получена вершина Y1 = (0, 0, 9, 2, 2, 9, 0, 0, 3, 0, 0, 5). Т.к. Z(Y1) = 119 < 141, полагаем Y0 := Y1 и начинаем пробу возможных перемещений вдоль ребер из найденной вершины многогранника решений в вершину с меньшим значением целевой функции:

Запишем вновь аналогично (5.8) и (5.9) систему уравнений, решением которой является вершина Y0, отметив в ней "отсутствующие" столбцы:
 | (5.11) |
y1 = 0, y2 = 0, y7 = 0, y8 = 0, y10 = 0, y11 = 0. (5.12)
Начнем движение по ребрам из данной вершины. Для этого будем исключать из (5.12) одно из уравнений, а оставшуюся систему будем решать совместно с не вошедшими в (5.12) уравнениями:
y3 = 0, y4 = 0, y5 = 0, y6 = 0, y9 = 0, y12 = 0. (5.13)
При этом надо учесть, что могут формироваться ранее исследованные комбинации нулей. (Комбинации нулей удобно метить индексным кодом, который следует запоминать для исключения повторного анализа.)
Положим в (5.13) y3 = 0 вместо y1 = 0. Последняя строка матрицы A станет нулевой.
Замена y1 = 0 уравнением y4 = 0 приводит к системе

Решаем с помощью подстановок, находим Y1 = (2, 0, 9, 0, 2, 9, 0, 0, 3, 0, 0, 5). Т.к. Z(Y1) = 127 > 119, найденную вершину отвергаем.
Примечание. Нам вновь не пришлось воспользоваться схемой Гаусса. По-видимому, вид уравнений и вхождение каждой переменной не более чем в два уравнения позволяют довольствоваться простой подстановкой. Ниже мы исследуем это подробнее.
Переходим к другому ребру, заменяя в (5.12) уравнение y2 = 0 уравнениями из (5.13).
Замена y3 = 0 вместо y2 = 0 приводит к тому, что последняя строка матрицы A становится нулевой.
Замена y4 = 0 вместо y2 = 0 приводит к системе уравнений

Находим с помощью подстановок Y1 = (0, 2, 9, 0, 4, 7, 0, 0, 1, 0, 0, 7). Т.к. Z(Y1) = 127 > 119, найденную вершину отвергаем и переходим к анализу следующего ребра.
Замена y3 = 0 вместо y7 = 0 приводит к тому, что в первом уравнении (9.25) не выполняется условие по ограничению y4 (y4 = 7).
Замена y4 = 0 вместо y7 = 0 приводит к тому, что в первом же уравнении (9.25) не выполняется условие по ограничению y3 (y3 = 9).
Замена y5 = 0 вместо y7 = 0 приводит к системе

Находим Y1 = (0, 0, 7, 4, 0, 9, 2, 0, 5, 0, 0, 3). Однако Z(Y1) = 129 > 119.
Переходим к анализу следующего ребра, поочередно заменяя уравнениями из (5.13) уравнение y8 = 0 из (5.11).
Замена y3 = 0 вместо y8 = 0 приводит к образованию последней нулевой строки матрицы A.
Замена y4 = 0 вместо y8 = 0 приводит к тому, что в первом уравнении не выполняется условие по ограничению y3 (y3 = 9).
Замена y5 = 0 вместо y8 = 0 приводит к системе

Находим Y1 = (0, 0, 9, 2, 0, 9, 0, 2, 5, 0, 0, 3). Т.к. Z(Y1) = 141 > 119, найденную вершину отвергаем.
Переходим к анализу следующего ребра, поочередно заменяя уравнениями из (5.13) уравнение y10 = 0 из (5.11).
Замена y3 = 0 вместо y10 = 0 приводит к тому, что в первом уравнении (5.11) не выполняется условие по ограничению y4 (y4 = 7).
Замена y4 = 0 вместо y10 = 0 приводит к тому, в первом же уравнении (5.11) не выполняется условие по ограничению y3 (y3 = 9).
Замена y5 = 0 вместо y10 = 0 приводит к тому, что во втором уравнении (5.11) не выполняется условие по ограничению y6 (y6= 9).
Замена y6 = 0 вместо y10 = 0 приводит к тому, что во втором же уравнении (5.11) не выполняется условие по ограничению y5 (y5 = 5).
Замена y9 = 0 вместо y10 = 0 приводит к системе

Находим Y1 = (0, 0, 9, 2, 5, 6, 0, 0, 0, 3, 0, 5). Т.к. Z(Y1) = 104 < 119, "перемещаемся" в найденную вершину с меньшим значением целевой функции.
Новая вершина характеризуется системой уравнений
y1 = 0, y2 = 0, y7 = 0, y8 = 0, y9 = 0, y11 = 0. (5.14)
Перепишем систему (5.11), выделив "отсутствующие" столбцы, вследствие (5.14):
 | (5.15) |
y3 = 0, y4 = 0, y5 = 0, y6 = 0, y10 = 0, y12 = 0 (5.16)
Замена y1 = 0 на y3 = 0 приводит к появлению (последней) нулевой строки матрицы A.
Замена y4 = 0 вместо y1 = 0 приводит к системе

Отсюда Y1 = (2, 0, 9, 0, 3, 8, 0, 0, 0, 1, 0, 7). Т.к. Z(Y1) = 114 > 104, исследуем следующее ребро, исключив в системе (5.14) уравнение y2 = 0 и заменяя его последовательно уравнениями из (5.16).
Замена y4 = 0 вместо y2 = 0 приводит к системе

Находим Y1 = (0, 2, 9, 0, 5, 6, 0, 0, 0, 1, 0, 7). Т.к. Z(Y1) = 114 > 104, исследуем следующее ребро, исключив в системе (5.14) уравнение y7 = 0 и заменяя его последовательно уравнениями из (5.16).
Замена y3 = 0 вместо y7 = 0 приводит к тому, что в первом уравнении (9.29) не выполняется условие по ограничению y4 (y4 = 7).
Замена y4 = 0 вместо y7 = 0 приводит к тому, что в первом же уравнении (9.29) не выполняется условие по ограничению y3 (y3= 9).
Замена y5 = 0 вместо y7 = 0 приводит к формированию нулевой (четвертой) строки матрицы A.
Замена y6 = 0 вместо y7 = 0 приводит к формированию нулевой (пятой) строки матрицы A.
Замена y10 = 0 вместо y7 = 0 приводит к тому, что в третьем уравнении (5.15) не выполняется условие по ограничению y12
(y12 = 7).
Замена y12 = 0 вместо y7 = 0 приводит к системе

Находим Y1 = (0, 0, 4, 7, 5, 1, 5, 0, 0, 8, 0, 0). Т.к. Z(Y1) = 104 и это не меньше уже полученной оценки, исследуем следующее ребро, исключив в системе (5.14) уравнение y8 = 0 и заменяя его последовательно уравнениями из (5.16).
Замена y3 = 0 вместо y8 = 0 приводит к образованию нулевой (шестой) строки матрицы A.
Замена y4 = 0 вместо y8 = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y3 (y3 = 9).
Замена y5 = 0 вместо y8 = 0 приводит к образованию нулевой (четвертой) строки матрицы A.
Замена y6 = 0 вместо y8 = 0 приводит к тому, что в пятом уравнении (5.15) не выполняется условие по ограничению y10 (y10= 8).
Замена y10 = 0 вместо y8 = 0 приводит к тому, что в третьем уравнении (5.15) не выполняется условие по ограничению y12 (y12 = 7).
Замена y12 = 0 вместо y8 = 0 приводит к системе

Ее решение Y1 = (0, 0, 9, 2, 5, 1, 0, 5, 0, 8, 0, 0) определяет значение Z(Y1) = 134 > 104.
Продолжаем перебор по следующему ребру.
Замена y3 = 0 вместо y9 = 0 приводит к образованию нулевой (шестой) строки матрицы A.
Замена y4 = 0 вместо y9 = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y3 (y3 = 9).
Замена y5 = 0 вместо y9 = 0 приводит к тому, что во втором уравнении (5.15) не выполняется условие по ограничению y6 (y6= 9).
Замена y6 = 0 вместо y9 = 0 приводит к тому, что во втором же уравнении (5.15) не выполняется условие по ограничению y5 (y5 = 5).
Замена y10 = 0 вместо y9 = 0 приводит к системе

Ее решение Y1 = (0, 0, 9, 2, 2, 9, 0, 0, 3, 0, 0, 5) определяет значение Z(Y1) = 119 > 104.
Приступаем к анализу следующего ребра, исключая в (5.14) уравнение y11 = 0 и заменяя его последовательно уравнениями из (5.16).
Замена y3 = 0 вместо y11 = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y4 (y4 = 7).
Замена y4 = 0 вместо y11 = 0 приводит к тому, что в первом уравнении (5.15) не выполняется условие по ограничению y3 (y3 = 9).
Замена y5 = 0 вместо y11 = 0 приводит к тому, что во втором уравнении (5.15) не выполняется условие по ограничению y6 (y6 = 9).
Замена y6 = 0 вместо y11 = 0 приводит к тому, что во втором же уравнении (5.15) не выполняется условие по ограничению y5 (y5 = 5).
Замена y10 = 0 вместо y11 = 0 приводит к системе
 | (5.17) |
Система не имеет решения, т.к. ранг матрицы системы не равен рангу расширенной матрицы.
Примечание. В несложном примере это легко обнаружить: вторая строка матрицы равна сумме четвертой и пятой строк, что противоречит соотношению между соответствующими свободными членами, 9 + 5

11. По-видимому, это говорит в пользу применения схемы Гаусса. В противном случае мы должны контролировать последовательно получаемые решения на удовлетворение тем соотношениям, которые в его получении не участвовали. Так, из четвертого и пятого уравнений имеем y5 = 5, y6 = 9. Но в соответствии со вторым уравнением y5 + y6 = 11. В то же время, совершая подстановку во второе уравнение, мы получаем нулевую левую часть, т.е.
нулевую строку матрицы A, что опять говорит в пользу подстановок!
Замена y12 = 0 вместо y11 = 0 приводит к системе

Ее решение Y1 = (0, 0, 4, 7, 5, 6, 0, 0, 0, 3, 5, 0) определяет значение целевой функции Z(Y1) = 89 < 104.
Полагаем Y0 := Y1. Теперь мы должны перемещаться по ребрам из вновь найденной вершины в поисках вершины с еще меньшим значением целевой функции. Придется перебрать до 6 ? 6 = 36 вариантов такого перемещения. Однако, достигнув ответа задачи в [15], положимся на его правильность и прекратим рассмотрение примера.
Постановка задачи и планы решения
Пусть [15] в пунктах A1, A2, ... ,Am производят некоторый однородный продукт в объеме ai (i=1, 2, ... , m) единиц. В пунктах B1, B2, ... ,Bn этот продукт потребляется в объеме bj
( j=1, 2, ... , n) единиц. Из каждого пункта производства {Ai} возможна транспортировка в любой пункт потребления Bj. Транспортные издержки} по перевозке из пункта Aiв пункт Bjединицы продукции равны cij (i=1, ... , m; j=1, ... , n).
Необходимо найти такой план перевозок, при котором запросы всех потребителей полностью удовлетворены, весь продукт из пунктов производства вывезен и суммарные транспортные издержки минимальны.
Пусть xij— количество продукта, перевозимого из пункта Aiв пункт Bj. Требуется найти значение переменных (перевозок) xij

 |
(5.1) |
при ограничениях
 |
(5.2) |
при условии неотрицательности
xij

и баланса
 |
(5.4) |
Как известно, условие баланса приводит к линейной зависимости уравнений в системе (5.2), ранг ее матрицы равен m+n-1.
Сформулируем задачу линейного программирования в канонической постановке, исключив из (5.2) одно уравнение. При этом мы считаем, что условие баланса (5.4) оказывает влияние на корректность постановки задачи и учтено при этой постановке. Исключенное уравнение будем использовать также для контроля получаемого решения.
Следуя плану параллельного решения задачи линейного программирования и учитывая, что оптимальное решение находится хотя бы в одной из вершин многогранника допустимых решений, образуемого ограничениями и условиями, сформируем это множество граней. В его состав войдут m+n-1 выделенных уравнений-ограничений и m ? n равенств нулю переменных на основе неотрицательности решения. Выбирая из этой системы по m ? n уравнений с обязательным участием всех выделенных уравнений-ограничений и решая их совместно, мы можем находить вершины многогранника решений.
Так мы можем реализовать метод прямого перебора. Количество вариантов составляет Cm ? nm ? n - (m + n - 1) . Это — количество различных способов приравнивания нулю m ? n-(m+n-1) переменных из их общего числа m ? n.
Мы можем реализовать и аналог симплекс-метода, найдя первоначально некоторую вершину, а затем перемещаясь по ребрам в одну из смежных вершин с большим значением целевой функции, пока это возможно.
Пусть dij — пропускная способность коммуникации (i, j), что порождает ограничение
xij

(5.18)
для всех i, j.
Тогда важная в практическом отношении задача заключается в минимизации (5.1) — целевой функции Z при ограничениях (5.2), (5.3), (5.4) и (5.18). Очевидно, что для разрешимости T -задачи должны выполняться условия
 |
(5.19) |
 |
(5.20) |
Как видим, данную задачу тоже можно решать прямым перебором вершин R с учетом резко увеличившегося числа уравнений его границ: их число, с учетом линейной зависимости, составляет теперь n+m-1+2(m? n). С учетом границ на основе условий неотрицательности решения, общее число испытываемых систем линейных уравнений составит C2(m ? n)m ? n - (m + n - 1).
Однако при этом переборе мы будем исследовать явно несовместимые варианты компоновки систем — а именно, варианты, включающие пары уравнений вида xij=0 и xij=dij. Тогда поступим иначе.
Сначала будем выбирать комбинации переменных, участвующих в формировании указанных систем линейных уравнений. Всех таких комбинаций будет Cm ? nm ? n - (m + n - 1). После выбора очередной комбинации переменных определим комбинацию их значений — 0 или значение пропускной способности. Таких комбинаций для выбранного набора m ? n - (m + n) - 1 переменных будет 2m ? n - (m + n - 1) .
Таким образом, общее число испытываемых систем линейных уравнений составит Cm ? nm ? n - (m + n - 1) ? 2m ? n - (m + n - 1) .
Воспользуемся и здесь параллельным аналогом симплекс-метода, найдя первоначально некоторую вершину многогранника решений, а затем пытаясь "переместиться" в смежную вершину с меньшим значением целевой функции.
Сделаем важное замечание. Будем считать, что если вдоль прямой, отрезком которой является исходящее из вершины L ребро, найдена смежная вершина M, то на этой же прямой, "в другую сторону" от L, нет смежных вершин. Т.е. одна прямая может связывать не более двух вершин многогранника решений. Предположим, что три вершины M, L, N лежат на одной прямой. Т.к. L — вершина, то существует хотя бы еще одно исходящее из нее ребро. Пусть оно соединяет L с вершиной K. Тогда построим плоскость, проходящую через три точки M, N, K, т.е. через точку K и прямую MN, которой принадлежит точка L. Плоскость поглотила как точку L, так и новое ребро, существование которого мы предположили.
Это означает, что если мы нашли смежную вершину "с одной стороны" по прямой, отрезком которой является исходящее ребро, то искать смежную вершину "с другой стороны" по этой же прямой не следует.
Этим предположением мы пользовались в предыдущем разделе, прекращая дальнейший поиск других смежных вершин вдоль прямой в случае, если одна такая вершина оказывается найденной. Здесь же это замечание, в частности, означает, что если мы нашли смежную данной вершину со значением xij = 0 ( xij = dk ), то испытывать значение xij = dk ( xij = 0 ) не следует. Т.е., как и ранее, мы вдоль каждого исходящего ребра будем искать единственную смежную вершину.
и ранее, линейное множество переменных
Введем, как и ранее, линейное множество переменных и сформулируем задачу:
Z = 2y1 + 3y2 + 3y3 + 2y4 + 2y5 + y6

при ограничениях
y1 + y2 + y3 = 12
y4 + y5 + y6 =10 (5.21)
y1+ y4 =7
y2 + y5 =7
y3 + y6 = 8
и при условии
0












Сформируем ограничения каждой переменной: y1 = min{12, 7, 4} = 4, аналогично y2 = 4, y3 = 5, y4 = 4, y5 = 4, y6 = 3. Исключим из рассмотрения последнее уравнение (5.21) и запишем уравнения всех потенциальных граней на основе (5.22):
y1 + y2 + y3 = 12
y4 + y5 + y6 = 10(5.23)
y1 + y4 = 7
y2 + y5 = 7
y1 = 0; y1 = 4
y2 = 0; y2 = 4
y3= 0; y3 = 5 (5.24)
y4 = 0; y4 = 4
y5 = 0; y5 = 4
y6 = 0; y6 = 3
Начнем перебор систем по шесть граней в поисках координат одной из вершин многогранника решений. В каждой такой системе должны присутствовать все уравнения (5.23) и два уравнения с разными переменными из (5.24).
Для формирования первой системы уравнений пробуем добавить к (5.23) уравнение y1 = 0. В результате в третьем уравнении не выполняется ограничение по y4 (y4 = 4).
Пробуем вариант y1 = 4. Совершив подстановку, убеждаемся, что он не приводит к подобному противоречию.
Полагаем y2 = 0. В первом уравнении не выполняется ограничение по y3 (y3 = 5).
Полагаем y2 = 4. Получаем и решаем систему уравнений
y1 + y2 + y3 = 12
y4 + y5 + y6 = 10
y1 + y4 = 7
y2 + y5 = 7
y1= 4
y2 = 4.
Находим Y = (4, 4, 4, 3, 3, 4). Однако данная точка не является вершиной многогранника решений, т.к. y6 = 4 противоречит условию (5.22).
Испытываем уравнение y3 = 0. В первом уравнении нарушается ограничение по y1 + y2 (y1 + y2 = 8 < 12).
Испытываем уравнение y3 = 5. Решаем систему уравнений
y1 + y2 + y3 = 12
y4 + y5 + y6 = 10
y1 + y4 = 7
y2 + y5 = 7
y1 = 4
y3 = 5.
Находим Y0 = (4, 3, 5, 3, 4, 3). Решение удовлетворяет условиям задачи, следовательно, найденная точка — вершина многогранника решений. Находим значение целевой функции Z(Y0) = 49.
На основе (5.23) и (5.24) выпишем уравнения всех граней, которым удовлетворяет вершина Y0, т.е.
в стек первую строку матрицы
Продолжим исследование приведенной выше сети.
Заносим в стек первую строку матрицы S. Находим первый нуль после обязательного нуля в первой позиции. Этот нуль указывает, что каналы 1 и 2 взаимно независимы (параллельны). Складываем логически строки, соответствующие каналам 1 и 2. Получаем новую строку s1 в вершине стека

Она содержит нули правее позиции 2. Это говорит о том, что 1 и 2 не исчерпывают ПМВНК.
Находим первый нуль правее позиции 2 — нуль в позиции 3. Складываем логически s2 = s1


Строка в вершине стека содержит нули только в тех позициях, которые соответствуют образующим ее каналам 1, 2, 3. Это означает, что мы нашли ПМВНК {1, 2, 3}, т.е. некоторый разрез сети. Минимальный поток, проходящий через него, составляет d1 + d2 + d3.
Исключаем из стека строку s2 и в строке s1 испытываем следующий нуль правее позиции 2. Это нуль в позиции 4. Формируем новую вершину стека s3 = s1


Строка s3 содержит нули не только в позициях 1, 2, 4. Первый такой нуль правее позиции 4 — в позиции 7.
Формируем новую вершину стека s4 = s3


Строка s4 содержит нули только в позициях, соответствующих каналам, "участвующим" в ее формировании. Значит, найдено еще одно ПМВНК {1, 2, 4, 7}. Оно определяет разрез сети с пропускной способностью d1 + d2 + d4 + d7.
Исключаем s4 из стека. Следующий испытываемый нуль в строке s3 занимает позицию 8. Формируем новую вершину стека s5 = s3


Строка s5 содержит нули только в позициях 1, 2, 4, 8. Следовательно, найдено ПМВНК {1, 2, 4, 8} с пропускной способностью d1 + d2 + d4 + d8.
Исключаем s5 из стека. Находим, что в s3 все нули исследованы. Исключаем s3 из стека. В s1 следующий нуль, подлежащий испытанию, занимает позицию 7. Формируем новую вершину стека — строку s6 = s1


Строка s6 не содержит нулей правее позиции 7. Исключаем s6 из стека.
Следующий испытываемый нуль в s1 занимает позицию 8.